K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

7 tháng 11 2021
a: Xét ΔABC có
BE là đường cao
CF là đường cao
BE cắt CF tại H
Do đó: H là trực tâm của ΔABC
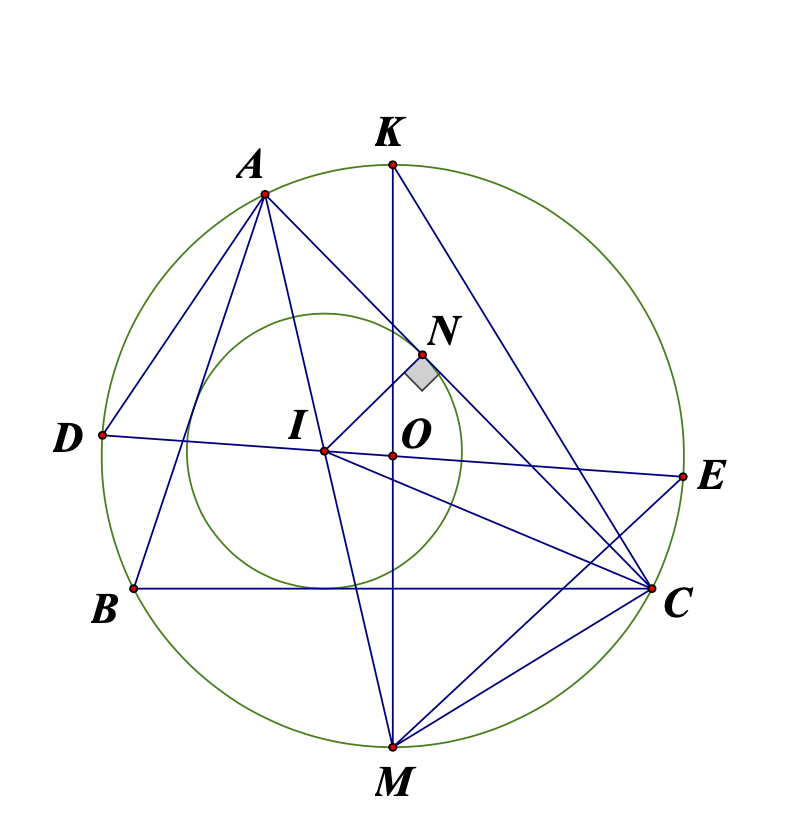

a) Vì ADME nội tiếp \(\Rightarrow\angle ADI=\angle IME\)
Xét \(\Delta IAD\) và \(\Delta IEM:\) Ta có: \(\left\{{}\begin{matrix}\angle AID=\angle EIM\\\angle ADI=\angle IME\end{matrix}\right.\)
\(\Rightarrow\Delta IAD\sim\Delta IEM\left(g-g\right)\Rightarrow\dfrac{IA}{IE}=\dfrac{ID}{IM}\Rightarrow IA.IM=ID.IE\)
ABMC nội tiếp \(\Rightarrow\angle MCB=\angle MAB=\dfrac{1}{2}\angle BAC\)
Ta có: \(\angle MCI=\angle MCB+\angle ICB=\dfrac{1}{2}\angle BAC+\dfrac{1}{2}\angle ACB\)
\(=\angle IAC+\angle ICA=\angle MIC\)
\(\Rightarrow\Delta MIC\) cân tại M \(\Rightarrow MI=MC\)
b) Kẻ \(OF\bot MC\Rightarrow F\) là trung điểm MC (\(\Delta OMC\) cân tại O)
\(\Rightarrow OF\) là phân giác \(\angle MOC\)
\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOC=\dfrac{1}{2}.2\angle MAC=\angle MAC\)
\(\Rightarrow sinMOF=sinMAC\)
Ta có: \(MC=2MF=2.\dfrac{MF}{MO}.MO=2.sinMOF.R=2RsinMAC\)