Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ABDC có
I là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AB=CD và AB//CD
b: ABDC là hình bình hành
=>BD//AC

a: Xét ΔABI và ΔACI có
AB=AC
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Xét ΔABI và ΔDCI có
AI=ID
\(\widehat{AIB}=\widehat{DIC}\)
IB=IC
Do đó: ΔABI=ΔDCI
Suy ra: AB=CD

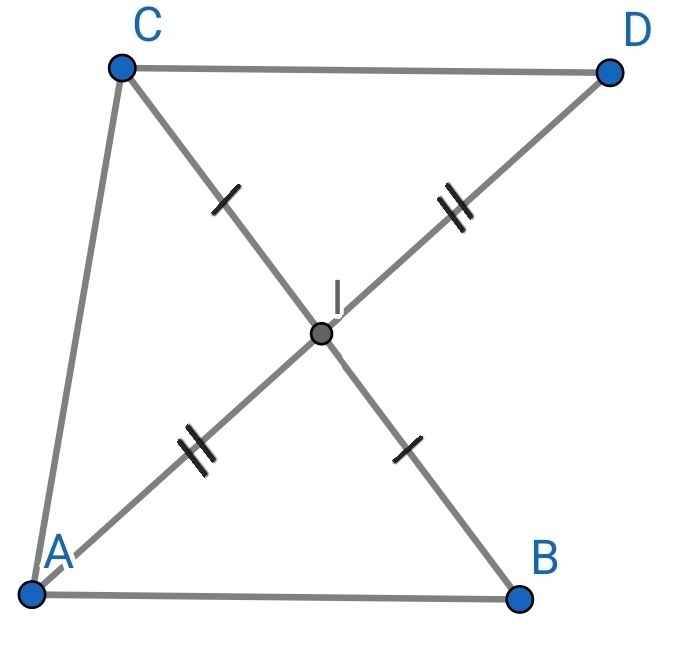 a) Xét ∆CDI và ∆BAI có:
a) Xét ∆CDI và ∆BAI có:
CI = BI (do I là trung điểm của BC)
∠CID = ∠BIA (đối đỉnh)
ID = IA (gt)
⇒ ∆CDI = ∆BAI (c-g-c)
⇒ CD = AB (hai cạnh tương ứng)
b) Do CD = AB (cmt)
Mà AB < AC (gt)
⇒ AC > CD
∆ACD có:
AC > CD (cmt)
⇒ ∠ADC > ∠CAD (quan hệ giữa góc và cạnh đối diện trong tam giác)
⇒ ∠IDC > ∠CAI
Do ∆CDI = ∆BAI (cmt)
⇒ ∠IDC = ∠BAI (hai góc tương ứng)
Mà ∠IDC > ∠CAI
⇒ ∠BAI > ∠CAI

a, I thuộc đường trung trực của AD (Gt)
=> IA = ID (Đl)
I thuộc đường trung trực của BC (gt)
=> IB = IC (đl)
b, xét ta giác IAB và tam giác IDC có : CD = AB (gt)
IB = IC (câu a)
IA = ID (câu a)
=> tam giác IAB = tam giác IDC (c-c-c)
A C B I D
a) I \(\in\) đường trung trực của BC
\(\Rightarrow IB=IC\)
I \(\in\) đường trung trực của AD
\(\Rightarrow IA=ID\Rightarrow\Delta IAD\) cân \(\Rightarrow\widehat{IAC}=\widehat{IDC}\) ( 1 )
Xét \(\Delta IAB\) và \(\Delta IDC\) có :
\(AB=CD\)
\(IB=IC\)
\(IA=ID\)
\(\Rightarrow\Delta IAB=\Delta IDC\)
\(\Rightarrow\widehat{BAI}=\widehat{CDI}\) ( 2 )
Từ (1) và (2) \(\Rightarrow\widehat{BAI}=\widehat{IAC}\Rightarrow AI\) là phân giác của \(\widehat{BAC}\)
XÉT \(\Delta IBA\) VÀ \(\Delta ICD\) CÓ
IB=IC (GT)
IA=ID (GT)
\(\widehat{AIB}=\widehat{DIC}\left(ĐỐI\right)ĐỈNH\)
=>\(\Delta IAB=\Delta ICD\left(CGC\right)\)
=>AB=AC (CTU/0