Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

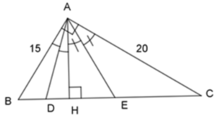
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
A B 2 + A C 2 = B C 2 ⇔ 15 2 + 20 2 = B C 2 ⇒ B C = 25
Ta có: S A B C = 1 2 .AB.AC = 1 2 .AH.BC ⇒ A H = A B . A C B C = 15.20 25 = 12
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
A B 2 = A H 2 + H B 2 ⇔ 15 2 = 12 2 + H B 2 ⇒ H B 2 = 81 ⇒ H B = 9 ⇒ H C = B C – H B = 25 – 9 = 16
Vì AE là phân giác của tam giác CAH nên: A C A H = C E E H ⇔ A C A H = C H − H E E H
ó 20 12 = − H E H E ó 20HE = 12(16 – HE) ó 20HE + 12HE = 12.16
ó 32HE = 192 ó HE = 6(cm)
Đáp án: B

Đoạn thẳng f: Đoạn thẳng [A, C] Đoạn thẳng h: Đoạn thẳng [B, A] Đoạn thẳng i: Đoạn thẳng [C, B] Đoạn thẳng n: Đoạn thẳng [A, H] Đoạn thẳng g_1: Đoạn thẳng [B, E] Đoạn thẳng i_1: Đoạn thẳng [A, F] Đoạn thẳng j_1: Đoạn thẳng [D, F] Đoạn thẳng k_1: Đoạn thẳng [A, G] A = (-0.43, -5.14) A = (-0.43, -5.14) A = (-0.43, -5.14) C = (21, -5.05) C = (21, -5.05) C = (21, -5.05) Điểm B: Điểm trên g Điểm B: Điểm trên g Điểm B: Điểm trên g Điểm H: Giao điểm của k, i Điểm H: Giao điểm của k, i Điểm H: Giao điểm của k, i Điểm D: Giao điểm của c, i Điểm D: Giao điểm của c, i Điểm D: Giao điểm của c, i Điểm F: Giao điểm của b, f_1 Điểm F: Giao điểm của b, f_1 Điểm F: Giao điểm của b, f_1 Điểm E: Giao điểm của b, f Điểm E: Giao điểm của b, f Điểm E: Giao điểm của b, f Điểm M: Trung điểm của g_1 Điểm M: Trung điểm của g_1 Điểm M: Trung điểm của g_1 Điểm G: Giao điểm của h_1, i Điểm G: Giao điểm của h_1, i Điểm G: Giao điểm của h_1, i
Cô hướng dẫn nhé
a) \(\Delta DEC\sim\Delta AEF\left(g-g\right)\)
b) Từ định lý Pi-ta-go ta tìm được BC = 5 cm.
\(\Delta ABH\sim\Delta CBA\left(g-g\right)\Rightarrow\frac{AB}{BC}=\frac{AH}{AC}=\frac{BH}{BA}\Rightarrow\frac{3}{5}=\frac{AH}{4}=\frac{BH}{3}\)
Vậy thì AH = 2,4 cm, BH = 1,8 cm. Khi đó BD - BH + HD = BH + AH = 2,4 + 1,8 = 4,2 cm.
\(S_{ABD}=\frac{1}{2}.AH.BD=\frac{1}{2}.2,4.4,2=5.04\left(cm^2\right)\)
c) Ta cm được AG là phân giác, từ đó suy ra \(\frac{GB}{GC}=\frac{AB}{AC}\) (TC tia phân giác)
Mà \(\frac{AB}{AC}=\frac{AH}{HC}=\frac{HD}{HC}\) (TC tam giác đồng dạng)
Vậy \(\frac{GB}{GC}=\frac{HD}{HC}\)

a, Xét tg ABC và tg ABH:
H=B=90
 góc chung
=> tg ABC đồng dạng tg ABH
b, Vì tg ABC đồng dạng với tg ABH.
Nên: AB/AH=AC/AB
=>AB^2=AH.AC
=>AB^2=4.13
=>AB=7,2cm
c, Hình như đề sai.

a) tính BC:
Áp dụng định lí Py-tago vào \(\Delta\)vuông ABC
ta có: BC2=BA2+AC2
=>BC2= 62+82
=> BC2= 36+64
=>BC2= 100
=> BC= \(\sqrt{100}\)
=> BC= 10 (cm)
b)c/m \(\Delta\)HAB đồng dạng \(\Delta\)HCA:
Ta có: - tam giác HAB đồng dạng với tam giác ABC ( \(\widehat{B}\)chung)
- tam giác HAC đồng dạng với tam giác ABC ( \(\widehat{C}\)chung)
=> \(\Delta HAB\)đồng dạng \(\Delta HCA\)( cùng đồng dạng \(\Delta ABC\))
có bạn nào giúp minh câu c và d được k. mình k cho
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
A B 2 + A C 2 = B C 2 ⇔ 15 2 + 20 2 = B C 2 ⇒ B C = 25
Ta có: S A B C = 1 2 .AB.AC = 1 2 .AH.BC ⇒ A H = A B . A C B C = 15.20 25 = 12
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
A B 2 = A H 2 + H B 2 ⇔ 15 2 = 12 2 + H B 2 ⇒ H B 2 = 81 = > H B = 9 ⇒ H C = B C – H B = 25 – 9 = 16
Vì AD là phân giác của tam giác ABH nên: A B A H = B D D H ⇔ A B A H = B H − D H D H
⇔ 15 12 = 9 − D H D H ó 15DH = 108 – 12DH ó DH = 4cm
Đáp án: A