Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(c,Chox^4+2x^2=0\)
\(x^2\left(x^2+2\right)=0\)
\(x^2+2=0\)
\(x^2=\left(-2\right)\)
\(x=\sqrt{-2}\)
\(\text{Vậy x = }\sqrt{12}\text{ là nghiệm của đa thức }x^4+2x^2\)
\(d,Chox^2+9x+20=0\)
\(x\left(x+9\right)+20=0\)
\(x\left(x+9\right)+20\left(x+9\right)=0\)
\(\left(20+x\right)+\left(x+9\right)=0\)
\(\Rightarrow\hept{\begin{cases}20+x=0\\x+9=0\end{cases}}\Rightarrow\hept{\begin{cases}x=-20\\x=-9\end{cases}}\)
\(\text{Vậy x = -20; x = -9 là nghiệm của đa thức }x^2+9x+20\)
\(e,Chox^2-x-20=0\)
\(x\left(x-1\right)-20=0\)
\(x\left(x-1\right)-20\left(x-1\right)=0\)
\(\left(x-20\right)\left(x-1\right)=0\)
\(\Rightarrow\hept{\begin{cases}x-20=0\\x-1=0\end{cases}\Rightarrow\hept{\begin{cases}x=20\\x=1\end{cases}}}\)
\(\text{Vậy x = 20; x = 1 là nghiệm của đa thức }x^2-x-20\)
\(f,Cho2x^2+5x+3=0\)
\(x\left(2x+5\right)+3=0\)
\(x\left(2x+5\right)+3\left(2x+5\right)=0\)
\(\left(x+3\right)\left(2x+5\right)=0\)
\(\Rightarrow\hept{\begin{cases}x+3=0\\2x+5=0\end{cases}\Rightarrow\hept{\begin{cases}x=-3\\x=\frac{-5}{2}\end{cases}}}\)
\(\text{Vậy x = -3; x = -5/2 là nghiệm của đa thức }2x^2+5x+3\)

Theo đề bài, x và y là hai đại lượng tỉ lệ thuận nên y = kx
Mà khi x =-1 thì y = 2 nên 2 = k.(-1) ⇒⇒ k = -2
Ta điền vào bảng sau:
|
x |
-2 |
-1 |
1 |
3 |
4 |
|
y |
4 |
2 |
-2 |
-6 |
-8 |
x và y tỉ lệ thuận nên y = k.x
Từ đó ta tìm được y lần lượt là:
(-2).(-3) = 6 ; (-2) (-1) = 2;
(-2).1 = (-2) ; (-2).5 = -10
Ta được bảng sau
| x | -3 | -1 | 1 | 2 | 5 |
| y | 6 | 2 | -2 | -4 | -10 |

Câu 7:
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
b: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
hay ΔDFC cân tại D

a) Vì x và y là hai đại lượng tỉ lệ nghịch nên xy = a
Khi \(x=2;y=15\Rightarrow a=xy=2.15=30\Rightarrow y=\dfrac{30}{x}\)
Kết quả như sau:
|
x |
x1 = 2 |
x2 = 3 |
x3 = 5 |
x4 = 6 |
|
y |
y1 = 15 |
y2 = 10 |
y3 = 6 |
y4 = 5 |
|
xy |
x1y1 = 30 |
x2y2 = 30 |
x3y3 = 30 |
x4y4 = 30 |
b) \(x_1y_1=x_2y_2=x_3y_3=x_4y_4=30\)
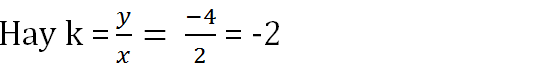
Tam giác `ABC` có \(\widehat{A}=64^0\)
Mà `AD` là tia phân giác của \(\widehat{BAC}\)
`->`\(\widehat{BAD}=\widehat{CAD}=\)`64/2=32^0`
Xét Tam giác `BAD:`
\(\widehat{BAD}+\widehat{ADB}+\widehat{ABD}=180^0 (\text {Định lý tổng 3 góc trong 1 tam giác})\)
\(32^0+\widehat{ADB}+80^0=180^0\)
`->`\(\widehat{ADB}=180^0-80^0-32^0=68^0\)
Xét các đáp án trên `->` \(\text{D. (t/m)}\)
Chọn D