Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi hai số dương là \(x\) và \(m-x\) (với \(0\le x\le m\)). Ta có tích của chúng là:
\(P=x\left(m-x\right)=mx-x^2\)
\(\Rightarrow P'=m-2x\)
Ta có: \(P'=0\Leftrightarrow x=\dfrac{m}{2}\) và \(P'\) đổi dấu từ dương sang âm tại \(x=\dfrac{m}{2}\) nên P đạt giá trị cực đại tại \(x=\dfrac{m}{2}\) và giá trị cực đại là: \(P=\dfrac{m}{2}\left(m-\dfrac{m}{2}\right)=\dfrac{m^2}{4}\)
So sánh với 2 giá trị đầu mút \(P\left(0\right)=0\) và \(P\left(m\right)=0\) thì thấy P lớn nhất bằng \(\dfrac{m^2}{4}\) khi \(x=\dfrac{m}{2}\).

Cho m > 0. Đặt x là số thứ nhất, 0 < x < m , số thứ hai là m – x
Xét tích P(x) = x(m – x)
Ta có: P’(x) = -2x + m
P′(x) = 0 ⇔ x = m/2
Bảng biến thiên
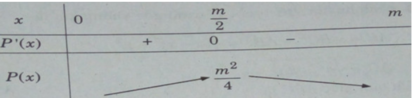
Từ đó ta có giá trị lớn nhất của tích hai số là: max P(x) = P(m/2) = m 2 /4

Ta có số có 2018 chữ số lớn nhất là 999....99 (2018 chữ số 9)
=> A lỡn nhất là 2018 x 9 = 18162
=> B lớn nhất là 1 + 8 + 1 + 6 + 2 = 18
=> C lớn nhất là 1 + 8 = 9
Ta có 3 x 9 + 2 = 29 mà 29 là số nguyên tố nên không tồn tại số như vậy

\(y'=3x^2-6mx=0\Rightarrow3x\left(x-2m\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2m\end{matrix}\right.\) (\(m\ne0\))
\(\Rightarrow\left[{}\begin{matrix}A\left(0;4m^2-2\right)\\B\left(2m;-4m^3+4m^2-2\right)\end{matrix}\right.\)
Bạn nên biết công thức này: công thức diện tích tam giác khi biết tọa độ 3 điểm:
\(S_{ABC}=\dfrac{1}{2}\left|\left(x_B-x_A\right)\left(y_C-y_A\right)-\left(x_C-x_A\right)\left(y_B-y_A\right)\right|\)
Áp nó vào bài toán:
\(\left|2m.\left(6-4m^2\right)-1.\left(-4m^3+4m^2-2\right)\right|=8\)
\(\Leftrightarrow...\)

\(z=\sqrt{3}+i=2\left(cos\dfrac{\pi}{6}+isin\dfrac{\pi}{6}\right)\\ \Rightarrow z^m=2^m\left(cos\dfrac{m\pi}{6}+isin\dfrac{m\pi}{6}\right)\)
\(z^m\) là số thực \(\Leftrightarrow sin\dfrac{m\pi}{6}=0\Leftrightarrow\dfrac{m\pi}{6}=0;\pi;2\pi;3\pi....\)
Vì m là só nguyên dương nhỏ nhất nên:
\(\dfrac{m\pi}{6}=\pi\Rightarrow m=6\)
Vậy m=6 thỏa mãn

Gọi số bé là x thì số lớn là x + 13. Tích của chúng là:
\(P=x\left(x+13\right)=x^2+13x\)
Ta có: \(P'=2x+13\)
\(P'=0\Leftrightarrow x=-\dfrac{13}{2}\) và \(P'\) đổi dấu từ âm sang dương tại \(x=-\dfrac{13}{2}\) nên P đạt cực tiểu tại \(x=-\dfrac{13}{2}\).
Vậy 2 số là: \(-\dfrac{13}{2}\) và \(-\dfrac{13}{2}+13=\dfrac{13}{2}\).
ọi số bé là n ta có số lớn là n+13
ta có: nx(n+13) phải là bé nhất
nx(n+13)
=n^2+13n
=(n^2+ 2xnx6,5+6,5^2)-6,5^2
=(n+6,5)^2-42,5. vì (n+6,5)^2>o nên
biểu thức trên nhỏ nhất khi n+6,5=0\Rightarrown=-6,5\Rightarrow số lớn =6,5>vậy 2 số đó là 6,5 và -6,5

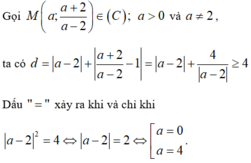
Cho m > 0. Đặt x là số thứ nhất, 0 < x < m , số thứ hai là m – x
Xét tích P(x) = x(m – x)
Ta có: P’(x) = -2x + m
P′(x) = 0 ⇔ x = m/2
Bảng biến thiên
Từ đó ta có giá trị lớn nhất của tích hai số là: max P(x) = P(m/2) = m 2 /4