Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) sin a=0,8
Ta có: \(\sin^2a+\cos^2a=1\)
\(\Rightarrow\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\orbr{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
\(\sin a=0,8\)
\(\sin^2a=1-\sin^2a=1\)
\(\cos^2a=1-\sin^2a=1-0,8^2=0,36\)
\(\Rightarrow\hept{\begin{cases}\cos a=0,6\\\cos a=-0,6\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\tan a=\frac{4}{3}\\\tan a=\frac{-4}{3}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\cot a=\frac{3}{4}\\\cot a=\frac{-3}{4}\end{cases}}\)
Code : Breacker

Làm tiêu biểu 1 bài thôi nhé. Các bài còn lại tương tự
a/ sin a = 0,8
Ta có: sin2 a + cos2 a = 1
=> cos2 a = 1 - sin2 a = 1 - 0,82 = 0,36
\(\Rightarrow\orbr{\begin{cases}cos\:a=0,6\\cos\:a=-0,6\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}tan\:a=\frac{4}{3}\\tan\:a=-\frac{4}{3}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}cot\:a=\frac{3}{4}\\cot\:a=-\frac{3}{4}\end{cases}}\)

Kẻ Đường cao AH
Tam giác AHB vuông tại H
=> \(sinB=\frac{AH}{AB}\) (1)
tam giác AHC vuông tại H
=> \(sinC=\frac{AH}{AC}\) (2)
Từ (1) và (2) => \(\frac{sinB}{sinC}=\frac{AH}{AB}:\frac{AH}{AC}=\frac{AC}{AB}\)
=> \(\frac{AC}{sinB}=\frac{AB}{sinC}\) (*)
CMTT : \(\frac{BC}{sinA}=\frac{AB}{sinC}\) (**)
\(\frac{BC}{sinA}=\frac{AC}{sinB}\) (***)
Từ (*) và (**) (***) => \(\frac{BC}{sinA}=\frac{AC}{sinB}=\frac{AB}{sinC}\)

Hướng dẫn giải:
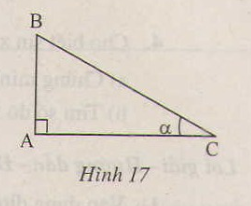
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
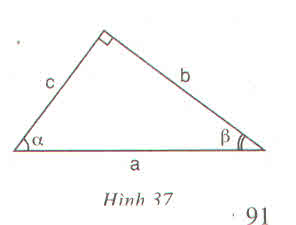
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khá
a) tgα=ABAC=AB⋅BCAC⋅BCtgα=ABAC=AB⋅BCAC⋅BC
⇒tgα=ABBC÷ACBC=sinαcosα⇒tgα=ABBC÷ACBC=sinαcosα
tgα⋅cotgα=ABAC⋅ACAB=1tgα⋅cotgα=ABAC⋅ACAB=1
cotgα=1tgα=1sinαcosα=cosαsinαcotgα=1tgα=1sinαcosα=cosαsinα
b) sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1sin2α+cos2α=AB2BC2+AC2BC2=BC2BC2=1
Nhận xét: Ba hệ thức tgα=sinαcosαtgα=sinαcosα
cotgα=cosαsinα;sin2α+cos2α=1cotgα=cosαsinα;sin2α+cos2α=1 là những hệ thức cơ bản bạn cần nhớ để giải một số bài tập khác.

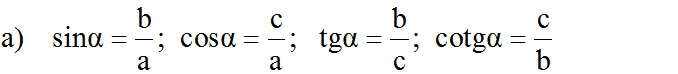
\(\cos\alpha=\sqrt{1-\dfrac{1}{25}}=\dfrac{2\sqrt{6}}{5}\)
\(\tan\alpha=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{12}\)
\(\cot\alpha=1:\dfrac{1}{2\sqrt{6}}=2\sqrt{6}\)