NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 5 2021
`M(x)=P(x)+Q(x)`
`=x^4-5x+2x^2+1+5x+x^2+5-3x^2+x^4`
`=2x^4+6`
Đặt `M(x)=0`
`<=>2x^4+6=0`
`<=>x^4=-3`(vô lý vì `x^4>=0`)
22 tháng 5 2021
a) Ta có M(x)=P(x)+Q(x)
=(\(x^4-5x+2x^2+1\))+(\(5x+x^2+5-3x^2+x^4\))
=\(x^4-5x+2x^2+1\)+\(5x+x^2+5-3x^2+x^4\)
=(\(x^4+x^4\))+(-5x+5x)+(\(2x^2\)+\(x^2\)-\(3x^2\))+(1+5)
=\(2x^4\)+6
Vậy M(x)=\(2x^4+6\)
b)Vì 2x\(^4\)\(\ge\) 0 với \(\forall\) x
nên \(2x^4+6\) \(\ge\)0 với \(\forall\)x
\(\Rightarrow\)M(x) \(\ge\) 0 với \(\forall\) x
Vậy M(x) vô nghiệm
27 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`a)`
\(P(x) = 5x^3 + 3 - 3x^2 + x^4 - 2x - 2 + 2x^2 + x\)
`= x^4 + 5x^3 + (-3x^2 + 2x^2) + (-2x+x) + (3-2)`
`= x^4 + 5x^3 - x^2 - x + 1`
\(Q(x) = 2x^4 + x^2 + 2x + 2 - 3x^2 - 5x + 2x^3 - x^4\)
`= (2x^4 - x^4) + 2x^3 + (x^2 - 3x^2) + (2x-5x) + 2`
`= x^4 + 2x^3 - 2x^2 - 3x +2`
`b)`
`P(x)+Q(x) = (x^4 + 5x^3 - x^2 - x + 1) + (x^4 + 2x^3 - 2x^2 - 3x +2)`
`= x^4 + 5x^3 - x^2 - x + 1 + x^4 + 2x^3 - 2x^2 - 3x +2`
`= (x^4+x^4)+(5x^3 + 2x^3) + (-x^2 - 2x^2) + (-x-3x) + (1+2)`
`= 2x^4 + 7x^3 - 3x^2 - 4x + 3`
`P(x)-Q(x)=(x^4 + 5x^3 - x^2 - x + 1) - (x^4 + 2x^3 - 2x^2 - 3x +2)`
`= x^4 + 5x^3 - x^2 - x + 1 - x^4 - 2x^3 + 2x^2 + 3x -2`
`= (x^4 - x^4) + (5x^3 - 2x^3) + (-x^2+2x^2)+(-x+3x)+(1-2)`
`= 3x^3 + x^2 + 2x - 1`
`Q(x)-P(x) = (x^4 + 2x^3 - 2x^2 - 3x +2)-(x^4 + 5x^3 - x^2 - x + 1)`
`= x^4 + 2x^3 - 2x^2 - 3x +2-x^4 - 5x^3 + x^2 + x - 1`
`= (x^4-x^4)+(2x^3 - 5x^3)+(-2x^2+x^2)+(-3x+x)+(2-1)`
`= -3x^3 - x^2 - 2x + 1`
`@` `\text {Kaizuu lv u.}`
S
17 tháng 6 2017
a) M(x) = (x4 - 5x + 2x2) + (5x + x2 + 5 - 3x2 + x4)
M(x) = x4 - 5x + 2x2 + 5x + x2 + 5 - 3x2 + x4
M(x) = 2x4 + 6
b) Ta thấy 2x4 \(\ge\) 0 \(\forall x\)
=> 2x4 + 6 \(\ge\)6 > 0 \(\forall x\)
Vậy M(x) vô nghiệm
CM
19 tháng 4 2017
Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có
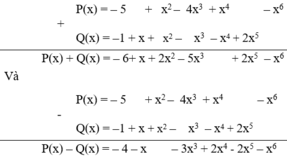
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6
P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6
DN
1
x^2 + x .
CM
28 tháng 8 2019
Ta có:
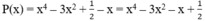
Vì : P(x) + Q(x) = x5 – 2x2 + 1
Suy ra Q(x) = x5 – 2x2 + 1– P(x).
3 tháng 4 2023
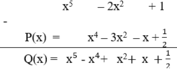
`a,`
`P(x)=5x^3+3-3x^2+x^4-2x-2+2x^2+x`
`P(x)=x^4+5x^3+(-3x^2+2x^2)+(-2x+x)+(3-2)`
`P(x)=x^4+5x^3-x^2-x+1`
`Q(x)=2x^4+x^2+2x+2-3x^2-5x+2x^3-x^4`
`Q(x)=(2x^4-x^4)+2x^3+(x^2-3x^2)+(2x-5x)+2`
`Q(x)=x^4+2x^3-2x^2-3x+2`
`b,`
`P(x)-Q(x)=(x^4+5x^3-x^2-x+1)-(x^4+2x^3-2x^2-3x+2)`
`P(x)-Q(x)= x^4+5x^3-x^2-x+1-x^4-2x^3+2x^2+3x-2`
`P(x)-Q(x)=(x^4-x^4)+(5x^3-2x^3)+(-x^2+2x^2)+(-x+3x)+(1-2)`
`P(x)-Q(x)=3x^3+x^2+2x-1`
a) P(x) + Q(x) = (x4 - 5x + 2x2 + 1) + (5x + 3x2 + 5 + 1/2x2)
= x4 - 5x + 2x2 + 1 + 5x + 3x2 + 5 +1/2x2
= x4 - (5x - 5x) + (2x2 + 3x2 + 1/2x2) + (1 + 5)
=x4 + 11/2x2 + 6
b) P(x) - Q(x) = (x4 - 5x + 2x2 + 1) - (5x + 3x2 + 5 + 1/2x2)
= x4 - 5x + 2x2 + 1 - 5x - 3x2 - 5 - 1/2x2
= x4 - (5x + 5x) + (2x2 - 3x2 - 1/2x2) + (1 - 5)
= x4 - 10x - 3/2x2 - 4
a) \(P\left(x\right)+Q\left(x\right)=x^4-5x+2x^2+1+5x+3x^2+5+\frac{1}{2}x^2\)
\(P\left(x\right)+Q\left(x\right)=x^4+\left(5x+5x\right)+\left(2x^2+3x^2+\frac{1}{2}x^2\right)+\left(1+5\right)\)
\(P\left(x\right)+Q\left(x\right)=x^4+10x+\frac{13}{x^2}+6\)
b) \(P\left(x\right)-Q\left(x\right)=\left(x^4-5x+2x^2+1\right)-\left(5x+3x^2+5+\frac{1}{2}x^2\right)\)
\(P\left(x\right)-Q\left(x\right)=x^4-5x+2x^2+1-5x-3x^2-5-\frac{1}{2}x^2\)
\(P\left(x\right)-Q\left(x\right)=x^4+\left(-5x-5x\right)+\left(2x^2-3x^2-\frac{1}{2}x^2\right)+\left(1-5\right)\)
\(P\left(x\right)-Q\left(x\right)=x^4-10x-\frac{3}{2}-6\)
Em mới lớp 3 thôi, sai đâu anh/chị thông cảm ạ