Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Gọi \(z_1,z_2\) là các nghiệm của phương trình với \(\left|z_1\right|=1\). Từ \(z_2=\frac{c}{a}.\frac{1}{z_1}\) kéo theo \(\left|z_2\right|=\left|\frac{c}{a}\right|.\frac{1}{\left|z_1\right|}=1\)
vì \(z_1+z_2=-\frac{b}{a},\left|a\right|=\left|b\right|\), ta có \(\left|z_1+z_2\right|^2=1\)
Hệ thức tương đương với
\(\left(z_1+z_2\right)\left(\overline{z_1}+\overline{z_2}\right)=1\) tức là \(\left(z_1+z_2\right)\left(\frac{1}{z_1}+\frac{1}{z_2}\right)=1\)
\(\left(z_1+z_2\right)^2=z_1z_2\)
hay \(\left(-\frac{b}{a}\right)^2=\frac{c}{a}\Rightarrow b^2=ac\)
b) Theo câu a) \(b^2=ac,c^2=ab\). Nhân các hệ thức được \(b^2c^2=a^2bc\Rightarrow a^2=bc\)
Do đó \(a^2+b^2+c^2=ab+bc+ca\)
Hệ tương đương với :
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
Tức là
\(\left(a-b\right)^2+\left(b-c\right)^2+2\left(a-b\right)\left(b-c\right)+\left(c-a\right)^2=2\left(a-b\right)\left(b-c\right)\)
Kéo theo
\(\left(a-c\right)^2=\left(a-b\right)\left(b-c\right)\)
Lấy giá trị tuyệt đối, được \(\beta^2=\gamma\alpha\)
Ở đây \(\alpha=\left|b-c\right|,\beta=\left|c-a\right|,\gamma=\left|a-b\right|\)
Tương tự được :
\(\alpha^2=\beta\gamma,\gamma^2=\alpha\beta,\)
Cộng các hệ thức, được :
\(\alpha^2+\beta^2+\gamma^2=\alpha\beta+\beta\gamma+\gamma\alpha\)
Tức là (\(\left(\alpha-\beta\right)^2+\left(\beta-\gamma\right)^2+\left(\gamma-\beta\right)^2=0\)
Do đó : \(\beta=\alpha=\gamma\)

Đặt z1 + z2 = a; z1. z2 = b; a, b ∈ R
Khi đó, z1 và z2 là hai nghiệm của phương trình
(z – z1)(z – z2) = 0 hay z2 – (z1 + z2)z + z1. z2 = 0 ⇔ z2 – az + b = 0
Đó là phương trình bậc hai đối với hệ số thực. Suy ra điều phải chứng minh.
TRONG VONG MAY PHUT MA GIAI MẤY BÀI LIỀN BẠN LÀ 1 SIÊU NHÂN GIẢI TOÁN...HOẶC BẠN LÀ 1 SIÊU NHÂN SAO CHÉP TỪ SÁCH GIẢI BÀI TẬP LÊN ĐỂ CẦU ...."GP"![]()

Một phương trình bậc hai nhận z và làm nghiệm là
(x - z)(x - ) = 0 hay x2 – (z +
)x + z
= 0.
Nếu z = a + bi thì z + = 2a, z
= a2 + b2
Vậy một phương trình bậc hai cần tìm là x2 – 2ax + a2 + b2 = 0

Trường hợp ∆ ≥ 0 ta đã biết kết quả.
Xét trường hợp ∆ < 0, từ công thức nghiệm
z1 = , z2 =
với |∆| = 4ac - b2
z1 + z2 =
z1 z2 =

Ta có:
f(x) = ax2 – 2(a + 1)x + a + 2 = (x – 1)(ax – a- 2) nên phương trình f(x) = 0 luôn có hai nghiệm thực là:
x = 1, x=a+2ax=a+2a
Theo định lí Vi-et, tổng và tích của các nghiệm đó là:
S=2a+2a,P=a+2aS=2a+2a,P=a+2a
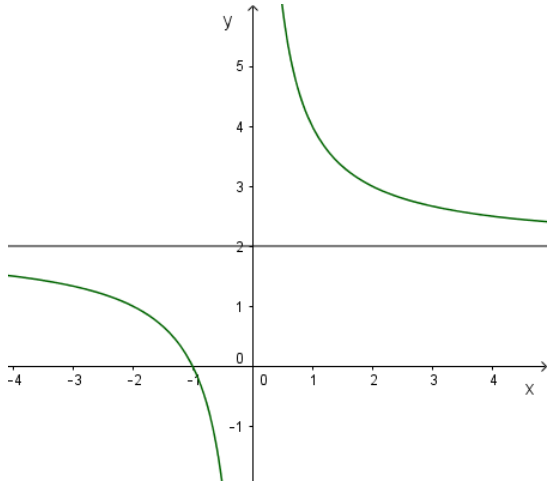
1. Khảo sát sự biến thiên và vẽ đồ thị hàm số S=2a+2a=2+2aS=2a+2a=2+2a
- Tập xác định : (-∞, 0)∪ (0, +∞)
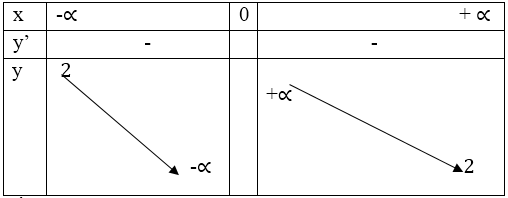
- Sự biến thiên: S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞)S′=−2a2<0,∀a∈(−∞,0)∪(0,+∞) nên hàm số nghịch biến trên hai khoảng (-∞, 0) và (0, +∞)
- Cực trị: Hàm số không có cực trị
- Giới hạn tại vô cực và tiệm cận ngang
lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2lima→+∞S=lima→+∞(2+2a)=2lima→−∞S=lima→−∞(2+2a)=2
Vậy S = 2 là tiệm cận ngang
- Giới hạn vô cực và tiệm cận đứng:
lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞lima→0+S=lima→0+(2+2a)=+∞lima→0−S=lima→0−(2+2a)=−∞
Vậy a = 0 là tiệm cận đứng.
- Bảng biến thiên:
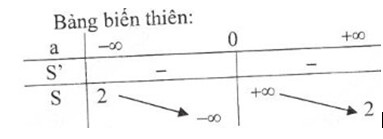
Đồ thị hàm số:
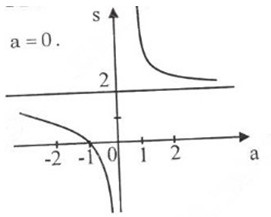
Đồ thị không cắt trục tung, cắt trục hoành tại a = -1
2) Khảo sát sự biến thiên và vẽ đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a
Tập xác định: D = R\{0}
S′=−2a2<0,∀a∈DS′=−2a2<0,∀a∈D
lima→0−S=−∞lima→0−S=−∞⇒ Tiệm cận đứng: a = 0
lima→±∞S=1lima→±∞S=1⇒ Tiệm cận ngang: S = 1
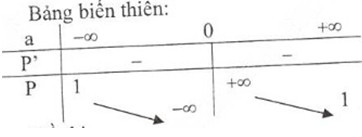
Đồ thị hàm số:
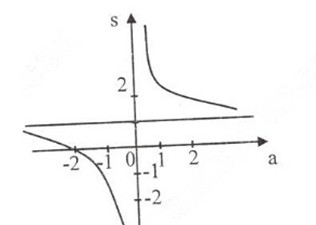
Ngoài ra: đồ thị hàm số P=a+2a=1+2aP=a+2a=1+2a có thể nhận được bằng cách tịnh tiến đồ thị S=2a+2a=2+2aS=2a+2a=2+2a dọc theo trục tung xuống phía dưới 1 đơn vị.
Gọi \(x_1,x_2\) là các nghiệm phương trình và \(r=\left|x_2\right|=\left|x_2\right|\) Khi đó :
\(\frac{p^2}{q^2}=\frac{\left(x_1+x_2\right)^2}{x_1x_2}=\frac{x_1}{x_2}+\frac{x_2}{x_1}+2=\frac{x_1\overline{x_2}}{r^2}+\frac{x_2\overline{x_1}}{r^2}+2=2+\frac{2}{r^2}Re\left(x_1\overline{x_2}\right)\)
Là số thực, hơn nữa :
\(Re\left(x_1\overline{x_2}\right)\ge-\left|x_1\overline{x_2}\right|=-r^2\)
Do đó \(\frac{p^2}{q^2}\ge0\)
vậy \(\frac{p}{q}\) là một số thực