Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử đường tròn đi qua điểm cố định có tọa độ \(\left(x_0;y_0\right)\)
\(\Rightarrow\) Với mọi m ta luôn có:
\(x_0^2+y_0^2+\left(m+2\right)x_0-\left(m+4\right)y_0+m+1=0\)
\(\Leftrightarrow m\left(x_0-y_0+1\right)+\left(x_0^2+y_0^2+2x_0-4y_0+1\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0-y_0+1=0\\x_0^2+y_0^2+2x_0-4y_0+1=0\end{matrix}\right.\)
\(\Rightarrow x_0^2+\left(x_0+1\right)^2+2x_0-4\left(x_0+1\right)+1=0\)
\(\Rightarrow2x_0^2-2=0\)
\(\Rightarrow\left\{{}\begin{matrix}x_0=1\Rightarrow y_0=2\\x_0=-1\Rightarrow y_0=0\end{matrix}\right.\)
Vậy đường tròn luôn đi qua 2 điểm cố định có tọa độ \(\left(1;2\right);\left(-1;0\right)\) với mọi m

\(PT\left(C\right):\left(x+1\right)^2+\left(y-7\right)^2=85\)
\(\Rightarrow\) Tâm \(I\left(-1;7\right)\) và bán kính là \(\sqrt{85}\)
PT tiếp tuyến qua \(M\left(1;-2\right)\Rightarrow x_0=1,y_0=-2\)
\(PT\) tiếp tuyến có dạng \(\left(a-x_0\right)\left(x-x_0\right)+\left(b-y_0\right)\left(y-y_0\right)=0\)
\(\Leftrightarrow\left(-1-1\right)\left(x-1\right)+\left(7+2\right)\left(y+2\right)=0\)
\(\Leftrightarrow-2\left(x-1\right)+9\left(y+2\right)=0\)
\(\Leftrightarrow-2x+2+9y+18=0\)
\(\Leftrightarrow-2x+9y+20=0\)

a) Ta có \(I\left( {2; - 3} \right)\) và \(R = \sqrt {{2^2} + {{\left( { - 3} \right)}^2} - \left( { - 12} \right)} = 5\)
b) Ta có: \({5^2} + {1^2} - 4.5 + 6.1 - 12 = 0\). Suy ra M thuộc \(\left( C \right)\). Tiếp tuyến d của (C) tại M có vectơ pháp tuyến là \(\overrightarrow {{n_d}} = \overrightarrow {IM} = \left( {3;4} \right)\), đồng thời d đi qua điểm \(M\left( {5;1} \right)\).
Vậy phương trình của d là \(3\left( {x - 5} \right) + 4\left( {y - 1} \right) = 0 \Leftrightarrow 3x + 4y - 19 = 0\).

a) Tâm I(2 ; -4), R = 5
b) Đường tròn có phương trình: (x – 2 )2 + (y + 4)2 = 25
Thế tọa độ A(-1 ; 0) vào vế trái, ta có :
(-1- 2 )2 + (0 + 4)2 = 32 + 42 = 25
Vậy A(-1 ;0) là điểm thuộc đường tròn.
Áp dụng công thức tiếp tuyến (Xem sgk)
Ta được pt tiếp tuyến với đường tròn tai A là:
(-1 – 2)(x – 2) + (0 + 4)(y + 4) = 25 <=> 3x – 4y + 3 = 0
Chú ý:
1. Theo tính chất tiếp tuyến với đường tròn tại 1 điểm thuộc đường tròn thì vuông góc với bán kính đi qua tiếp điểm, ta có thể giải câu này như sau:
Vectơ = (-3; 4)
Tiếp tuyến đi qua A(-1; 0) và nhận làm một vectơ pháp tuyến có phương trình:
-3(x + 1) + 4(y – 0) = 0 ,<=> 3x – 4y + 3 = 0

a) Đường tròn \({(x + 1)^2} + {(y - 5)^2} = 9\) có tâm \(I\left( { - 1;5} \right)\) và \(R = 3\)
b) Đường tròn \({x^2} + {y^2}-6x - 2y-{\rm{1}}5 = 0\) có tâm \(I\left( {3;1} \right)\) và \(R = \sqrt {{3^2} + {1^2} + 15} = 5\)

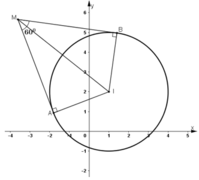
Gọi A, B là hai tiếp điểm của tiếp tuyến kẻ từ M đến (C).

Mà điểm I là cố định nên tập hợp các điểm M là đường tròn tâm I, bán kính R = 6 và có phương trình: (x – 1)2 + (y – 2)2 = 36.

1.
Ta có: \(m^2+\left(m-1\right)^2=2m^2-2m+1=\frac{1}{2}\left(2m-1\right)^2+\frac{1}{2}>0;\forall m\)
\(\Rightarrow\) Với mọi m pt đã cho là pt đường tròn
2.
\(R=\sqrt{\frac{1}{2}\left(2m-1\right)^2+\frac{1}{2}}\)
\(\Rightarrow R\ge\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}\)
\(R_{min}=\frac{\sqrt{2}}{2}\) khi \(m=\frac{1}{2}\)
3.
Đường tròn tâm \(I\left(x_I;y_I\right)\Rightarrow\left\{{}\begin{matrix}x_I=m\\y_I=m-1\end{matrix}\right.\)
\(\Rightarrow x_I-y_I=1\Leftrightarrow x_I-y_I-1=0\)
\(\Rightarrow\) Tập hợp tâm I là đường thẳng có pt \(x-y-1=0\)
4.
Gọi \(M\left(x;y\right)\) là điểm cố định mà đường tròn đi qua
\(\Rightarrow x^2+y^2-2mx-2my+2y=0\)
\(\Leftrightarrow x^2+y^2+2y-2m\left(x+y\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2+2y=0\\x+y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x^2+y^2+2y=0\\y=-x\end{matrix}\right.\)
\(\Rightarrow x^2+\left(-x\right)^2-2x=0\)
\(\Leftrightarrow x^2-x=0\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=0\\x=1\Rightarrow y=-1\end{matrix}\right.\)
\(\Rightarrow\) Đường tròn luôn đi qua 2 điểm cố định có tọa độ \(\left(0;0\right);\left(1;-1\right)\)
5.
Phương trình hoành độ giao điểm:
\(\left\{{}\begin{matrix}x^2+y^2-2mx-2\left(m-1\right)y=0\\x+y-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2+y^2-2mx-2\left(m-1\right)y=0\\y=1-x\end{matrix}\right.\)
\(\Rightarrow x^2+\left(1-x\right)^2-2mx-2\left(m-1\right)\left(1-x\right)=0\)
\(\Leftrightarrow2x^2-2x+1-2mx-\left(2m-2\right)\left(1-x\right)=0\)
\(\Leftrightarrow2x^2-4x-2m+3=0\)
\(\Delta'=4-2\left(-2m+3\right)=4m-2=0\Rightarrow m=\frac{1}{2}\)