Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bình phương hai vế của phương trình \(\sqrt {26{x^2} - 63x + 38} = 5x - 6\) ta được:
\(26{x^2} - 63x + 38 = {(5x - 6)^2}\)
\( \Leftrightarrow 26{x^2} - 63x + 38 = 25{x^2} - 60x + 36\)
\( \Leftrightarrow {x^2} - 3x + 2 = 0\)
\( \Leftrightarrow x = 1\) hoặc \(x = 2\)
b) Thử lại:
Với x = 1 thay vào phương trình đã cho ta được:
\(\sqrt {{{26.1}^2} - 63.1 + 38} = 5.1 - 6\)
\( \Leftrightarrow 1 = - 1\)(vô lý)
Với x=2 thay vào phương trình đã cho ta được:
\(\sqrt {{{26.2}^2} - 63.2 + 38} = 5.2 - 6\)
\( \Leftrightarrow \sqrt {16} = 4 \Leftrightarrow 4 = 4\) (luôn đúng)
Vậy giá trị x=2 thỏa mãn phương trình đã cho.

Nếu bình phương cả hai vế của bất phương trình ta được bất phương trình:\(1-x\le x^2\).
BPT này là bất phương trình hệ quả của bất phương trình ban đầu vì khi bình phương hai vế của bất phương trình thì hai vế phải luôn không âm.

Phương trình 3x = 2 (1) có nghiệm x = 2/3
Phương trình 2x = 3 (2) có nghiệm x = 3/2
Cộng các vế tương ứng của hai phương trình (1) và (2) ta được phương trình
3x + 2x = 2 + 3 hay 5x = 5 (3) có nghiệm x = 1.
a) Phương trình (3) không tương đương với phương trình nào trong các phương trình (1) và (2) vì không có cùng tập nghiệm.
b) Phương trình (3) không phải phương trình hệ quả của phương trình nào trong các phương trình (1) và (2) vì nghiệm của (1) và (2) đều không phải nghiệm của (3).

Nếu bình phương hai vế (khử căn thức chứa ẩn) của bất phương trình 1 - x ≤ x ta nhận được bất phương trình 1 - x ≤ x 2
Bất phương trình nhận được không tương đương với bất phương trình đã cho vì có x = 2 không phải là nghiệm bất phương trình đã cho nhưng lại là nghiệm của bất phương trình mới nhận được sau phép bình phương.
Ghi nhớ: Không được bình phương hai vế một bất phương trình vì có thể làm xuất hiện nghiệm ngoại lai.

Lời giải:
a/
PT $(1)$ có nghiệm $x=\frac{2}{3}$. PT $(2)$ có nghiệm $x=\frac{3}{2}$
Cộng 2 vế tương ứng của pt đã cho thì có:
$5x=5\Leftrightarrow x=1$
Vậy tập nghiệm của pt sau không giống 2 pt đầu nên câu trả lời là không.
b.
PT đó không phải hệ quả của 1 trong 2 PT ban đầu vì \(\left\{\frac{2}{3}\right\}\not\subset\left\{1\right\}; \left\{\frac{3}{2}\right\}\not\subset\left\{1\right\}\)

a) 3x = 2 ⇔ x = ;
2x =3 ⇔ x = .
Cộng các vế tương ứng của hai phương trình ta được 5x =5 ⇔ x = 1
Tập nghiệm của phương trình mới nhận sau phép cộng khác với các tập nghiệm của phương trình đã cho ban đầu. Vậy phương trình có được do cộng các vế tương ứng của hai phương trình đã cho không tương đương với phương trình nào.
b) Phương trình này cũng không phải là phương trình hệ quả của một trong hai phương trình. Bởi vì nghiệm của một trong hai phương trình đã cho không là nghiệm của phương trình mới.

Phương trình 4x = 5 (1) có nghiệm x = 5/4
Phương trình 3x = 4 (2) có nghiệm x = 4/3
Nhân các vế tương ứng của hai phương trình đã cho ta được phương trình
4x.3x = 5.4 hay 12x2 = 20 (3) có hai nghiệm x = 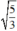 và x = -
và x = -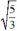
a) Phương trình (3) không tương đương với phương trình nào trong hai phương trình (1) và (2) vì không có cùng tập nghiệm.
b) Phương trình (3) không phải phương trình hệ quả của phương trình nào trong các phương trình (1) và (2) vì nghiệm của (1) và (2) đều không phải nghiệm của (3).

1.
\(2x+1\ge0\Rightarrow x\ge-\dfrac{1}{2}\)
Khi đó pt đã cho tương đương:
\(x^2+2x+2m=\left(2x+1\right)^2\)
\(\Leftrightarrow x^2+2x+2m=4x^2+4x+1\)
\(\Leftrightarrow3x^2+2x+1=2m\)
Xét hàm \(f\left(x\right)=3x^2+2x+1\) trên \([-\dfrac{1}{2};+\infty)\)
\(-\dfrac{b}{2a}=-\dfrac{1}{3}< -\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{2}\right)=\dfrac{3}{4}\) ; \(f\left(\dfrac{1}{3}\right)=\dfrac{2}{3}\)
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb khi và chỉ khi \(\dfrac{2}{3}< 2m\le\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{1}{3}< m\le\dfrac{3}{8}\)
\(\Rightarrow P=\dfrac{1}{8}\)
3.
Đặt \(x^2=t\ge0\Rightarrow\left[{}\begin{matrix}x=\sqrt{t}\\x=-\sqrt{t}\end{matrix}\right.\)
Pt trở thành: \(t^2-3mt+m^2+1=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=9m^2-4\left(m^2+1\right)>0\\t_1+t_2=3m>0\\t_1t_2=m^2+1>0\end{matrix}\right.\) \(\Rightarrow m>\dfrac{2}{\sqrt{5}}\)
Ta có:
\(M=x_1+x_2+x_3+x_4+x_1x_2x_3x_4\)
\(=-\sqrt{t_1}-\sqrt{t_2}+\sqrt{t_1}+\sqrt{t_2}+\left(-\sqrt{t_1}\right)\left(-\sqrt{t_2}\right)\sqrt{t_1}.\sqrt{t_2}\)
\(=t_1t_2=m^2+1\) với \(m>\dfrac{2}{\sqrt{5}}\)

1.
Đặt \(\sqrt{x^2-4x+5}=t\ge1\Rightarrow x^2-4x=t^2-5\)
Pt trở thành:
\(4t=t^2-5+2m-1\)
\(\Leftrightarrow t^2-4t+2m-6=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm pb đều lớn hơn 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=4-\left(2m-6\right)>0\\\left(t_1-1\right)\left(t_2-1\right)>0\\\dfrac{t_1+t_2}{2}>1\\\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}10-2m>0\\t_1t_2-\left(t_1+t_1\right)+1>0\\t_1+t_2>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< 5\\2m-6-4+1>0\\4>2\end{matrix}\right.\) \(\Leftrightarrow\dfrac{9}{2}< m< 5\)
2.
Để pt đã cho có 2 nghiệm:
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\\Delta'=1+4\left(m-3\right)\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne3\\m\ge\dfrac{11}{4}\end{matrix}\right.\)
Khi đó:
\(x_1^2+x_2^2=4\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\)
\(\Leftrightarrow\dfrac{4}{\left(m-3\right)^2}+\dfrac{8}{m-3}=4\)
\(\Leftrightarrow\dfrac{1}{\left(m-3\right)^2}+\dfrac{2}{m-3}-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{1}{m-3}=-1-\sqrt{2}\\\dfrac{1}{m-3}=-1+\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=4-\sqrt{2}< \dfrac{11}{4}\left(loại\right)\\m=4+\sqrt{2}\end{matrix}\right.\)
a) Bình phương hai vế của phương trình\(\sqrt {{x^2} - 3x + 2} = \sqrt { - {x^2} - 2x + 2} \)ta được:
\({x^2} - 3x + 2 = - {x^2} - 2x + 2\)(1)
Giải phương trình trên ta có:
\((1) \Leftrightarrow 2{x^2} - x = 0\)
\( \Leftrightarrow x(2x - 1) = 0\)
\( \Leftrightarrow x = 0\) hoặc \(x = \frac{1}{2}\)
b) Thử lại ta có:
Với x=0, thay vào phương trình đã cho ta được: \(\sqrt {{0^2} - 3.0 + 2} = \sqrt { - {0^2} - 2.0 + 2} \Leftrightarrow \sqrt 2 = \sqrt 2 \) (luôn đúng)
Với \(x = \frac{1}{2}\), thay vào phương trình đã cho ta được:
\(\sqrt {{{\left( {\frac{1}{2}} \right)}^2} - 3.\frac{1}{2} + 2} = \sqrt { - {{\left( {\frac{1}{2}} \right)}^2} - 2.\frac{1}{2} + 2} \Leftrightarrow \sqrt {\frac{3}{4}} = \sqrt {\frac{3}{4}} \) (luôn đúng)
Vậy các giá trị x tìm được ở câu a thỏa mãn phương trình đã cho.