Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giả sử hình thoi là ABCD với \(A\left(0;1\right)\)
Do tọa độ A thỏa \(x+7y-7=0\) nên đó là cạnh chứa A, ko mất tính tổng quát, giả sử đó là cạnh AB
Tọa độ A ko thỏa pt đường chéo nên đó là đường chéo BD
\(\Rightarrow\) Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x+7y-7=0\\x+2y-7=0\end{matrix}\right.\) \(\Rightarrow B\left(7;0\right)\)
Phương trình AC qua A vuông góc BD: \(2\left(x-0\right)-1\left(y-1\right)=0\Leftrightarrow2x-y+1=0\)
Tọa độ tâm I là nghiệm: \(\left\{{}\begin{matrix}x+2y-7=0\\2x-y+1=0\end{matrix}\right.\) \(\Rightarrow I\left(1;3\right)\)
I là trung điểm AC \(\Rightarrow C\left(2;5\right)\)
I là trung điểm BD \(\Rightarrow D\left(-5;-3\right)\)
Biết tọa độ các đỉnh, bạn tự viết pt các cạnh nhé
Từ giả thiết suy ra điểm A không nằm trên 2 cạnh có phương trình đã cho. Bởi vậy, đó là phương trình của 2 đường thẳng chứa cạnh BC, CD, chẳng hạn \(BC:2x-3y+5\)
\(CD:3x+2y-7=0\)
Khi đó, đường thẳng chứa cạnh AB đi qua \(A\left(2;-3\right)\) và song song với đường thẳng CD, nên có phương trình :
\(3\left(x-2\right)+2\left(y+3\right)=0\)
hay : \(3x+2y=0\) ẳng chứa cạnh AD là :
\(2x-3y-11=0\)
B là giao điểm của BD và AB nên tọa độ thỏa mãn:
\(\left\{{}\begin{matrix}x+2y-7=0\\x+7y-7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=7\\y=0\end{matrix}\right.\) \(\Rightarrow B\left(7;0\right)\)
Đường chéo AC qua A và vuông góc BD nên nhận (2;-1) là 1 vtpt
Phương trình AC:
\(2\left(x-0\right)-1\left(y-1\right)=0\Leftrightarrow2x-y+1=0\)
Gọi I là giao điểm AC và BD \(\Rightarrow\) I là tâm hình thoi, tọa độ I thỏa mãn:
\(\left\{{}\begin{matrix}2x-y+1=0\\x+2y-7=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\) \(\Rightarrow I\left(1;3\right)\)
I là trung điểm AC nên tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x_C=2x_I-x_A=2\\y_C=2y_I-y_A=5\end{matrix}\right.\) \(\Rightarrow C\left(2;5\right)\)
I là trung điểm BD nên tọa độ D thỏa mãn:
\(\left\{{}\begin{matrix}x_D=2x_I-x_B=-5\\y_D=2y_I-y_B=6\end{matrix}\right.\) \(\Rightarrow D\left(-5;6\right)\)
Lời giải:
$BD: x+2y-7=0; AD: x+3y-3=0$ nên $D$ chính là giao điểm của 2 PTĐT này.
\(\Rightarrow \left\{\begin{matrix} x_D+2y_D-7=0\\ x_D+3y_D-3=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x_D=15\\ y_D=-4\end{matrix}\right.\)
Vì $ABCD$ là hình thoi nên $AC\perp BD$.
$\Rightarrow \overrightarrow{AC}=\overrightarrow{n_{BD}}=(1,2)$
$\Rightarrow \overrightarrow{n_{AC}}=(-2,1)$
PTĐT $AC$ là:
$-2(x-0)+1(y-1)=0\Leftrightarrow -2x+y-1=0\Leftrightarrow 2x-y+1=0$
Gọi $O$ là giao 2 đường chèo $AC, BD$.
\(\Rightarrow \left\{\begin{matrix} 2x_O-y_O+1=0\\ x_O+2y_O-7=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x_O=1\\ y_O=3\end{matrix}\right.\)
$O$ là trung điểm $BD$ nên: $x_B=2x_O-x_D=2-15=-13$
$y_B=2y_O-y_D=6+4=10$
Vì $\overrightarrow{BC}=\overrightarrow{AD}$ nên PTĐT $BC$ có dạng:
$(x+13)+3(y-10)-3=0$
$\Leftrightarrow x+3y-30=0$
$O$ là trung điểm của $AC$ nên:
$x_C=2x_O-x_A=2-0=2$
$y_C=2y_C-y_A=6-1=5$
$\Rightarrow \overrightarrow{CD}=(13, -9)$
$\Rightarrow \overrightarrow{n_{CD}}=(9,13)$
PTĐT $CD$ là: $9(x-2)+13(y-5)=0\Leftrightarrow 9x+13y-83=0$
PTĐT $AB$ là: $9(x-0)+13(y-1)=0\Leftrightarrow 9x+13y-13=0$
Trực tâm H là giao điểm của BH và AH ⇒ tọa độ H là nghiệm của hệ:
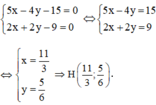
A là giao điểm của AB và AH nên tọa độ A là nghiệm của hệ phương trình:
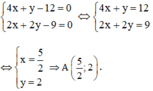
B là giao điểm BH và AB nên tọa độ điểm B là nghiệm của hệ:
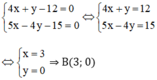
+ AC ⊥ HB, mà HB có một vtpt là (5; -4)⇒ AC nhận (4; 5) là một vtpt
AC đi qua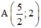 
⇒ Phương trình đường thẳng AC: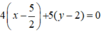 
hay 4x + 5y – 20 = 0.
+ CH ⊥ AB, AB có một vtpt là (4; 1) ⇒ CH nhận (1; -4) là một vtpt
CH đi qua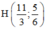 
⇒ Phương trình đường thẳng CH: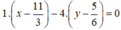 
hay CH: 3x – 12y - 1 = 0.
+ BC ⊥ AH , mà AH nhận (2; 2) là một vtpt
⇒ BC nhận (1; -1) là một vtpt
BC đi qua B(3; 0)
⇒ Phương trình đường thẳng BC: 1(x - 3) – 1(y – 0) = 0 hay x – y – 3 = 0.
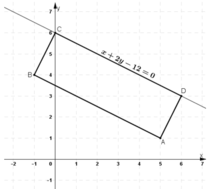
CD: x + 2y – 12 = 0 ⇒ CD nhận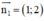 
là một vtpt
⇒ CD nhận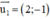 
là một vtcp.
+ ABCD là hcn ⇒ AD ⊥ CD ⇒ AD nhận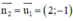 
là một vtpt
A(5 ; 1) ∈ AD
⇒ Phương trình đường thẳng AD: 2( x- 5) – 1(y – 1) = 0 hay 2x – y – 9 = 0.
+ ABCD là hcn ⇒ AB // CD ⇒ AB nhận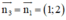 
là một vtpt
A(5;1) ∈ AB
⇒ Phương trình đường thẳng AB: 1( x- 5) + 2(y -1) = 0 hay x + 2y – 7 = 0
+ ABCD là hcn ⇒ BC ⊥ CD ⇒ BC nhận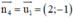 
là một vtpt
C(0, 6) ∈ CD
⇒ Phương trình đường thẳng BC: 2(x- 0)- 1(y – 6) =0 hay 2x – y + 6 = 0.
Giả sử phương trình AC là 2x-5y+6=0 và pt BC là 4x+7y-21=0
Phương trình đường cao AH qua H và vuông góc BC:
\(7\left(x-0\right)-4\left(y-0\right)=0\Leftrightarrow7x-4y=0\)
Pt đường cao BH qua H vuông AB: \(2x+5y=0\)
Tọa độ A là nghiệm: \(\left\{{}\begin{matrix}2x-5y+6=0\\7x-4y=0\end{matrix}\right.\) \(\Leftrightarrow A\left(-4;-7\right)\)
Tọa độ B là nghiệm \(\left\{{}\begin{matrix}4x+7y-21=0\\2x+5y=0\end{matrix}\right.\) \(\Rightarrow B\left(\dfrac{35}{2};-7\right)\)
Phương trình AB: \(y+7=0\)
cạnh thứ ba 2x-5y+3=0. cạnh thứ tư 2x-5y-26=0, đường chéo thứ hai 7x-3x-33=0