Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(3x^2-2\left(m+1\right)x+3m-5=0\)
Theo định lý Viet
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}\\x_1x_2=\dfrac{c}{a}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+1\right)}{3}\\x_1x_2=\dfrac{3m-5}{3}\end{matrix}\right.\)
Theo yêu cầu đề bài \(x_1=3x_2\)
\(\)\(\Rightarrow\left\{{}\begin{matrix}3x_2+x_2=\dfrac{2\left(m+1\right)}{3}\\3x^2_2=\dfrac{3m-5}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}4x_2=\dfrac{2\left(m+1\right)}{3}\\3x^2_2=\dfrac{3m-5}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\3x_2^2=\dfrac{3m-5}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\3\left(\dfrac{m+1}{6}\right)^2=\dfrac{3m-5}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\\dfrac{m^2+2m+1}{12}=\dfrac{3m-5}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\\dfrac{m^2+2m+1}{4}=3m-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\m^2+2m+1=12m-20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\m^2-10m+21=0\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\\left[{}\begin{matrix}m_1=7\\m_2=3\end{matrix}\right.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}m_1=7\Rightarrow\left\{{}\begin{matrix}x_1=4\\x_2=\dfrac{4}{3}\end{matrix}\right.\\m_2=3\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=\dfrac{2}{3}\end{matrix}\right.\end{matrix}\right.\)

Để phương trình có nghiệm thì \(\Delta\ge0\Leftrightarrow\left(m+1\right)^2-3\left(3m-5\right)\ge0\) \(\Leftrightarrow m^2-7m+16\ge0\)
\(\Leftrightarrow\left(m-\dfrac{7}{2}\right)^2+\dfrac{15}{4}\ge0\forall m\in R\).
Vậy phương trình luôn có nghiệm với mọi m.
Gọi \(x_1;x_2\) là nghiệm của phương trình, theo giả thiết ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+1\right)}{3}\\x_1=3x_2\\x_1.x_2=\dfrac{3m-5}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\x_1=\dfrac{m+1}{2}\\x_1.x_2=\dfrac{3m-5}{3}\end{matrix}\right.\) (1)
Từ (1) ta có: \(\dfrac{m+1}{6}.\dfrac{m+1}{2}=\dfrac{3m-5}{3}\Leftrightarrow\left(m-1\right)^2=4\left(3m-5\right)\)
\(\Leftrightarrow m^2-14m+21=0\Leftrightarrow\left[{}\begin{matrix}m=7-2\sqrt{7}\\m=7+2\sqrt{7}\end{matrix}\right.\)
Với \(m=7-2\sqrt{7}\) ta có:
\(x_1=\dfrac{m+1}{2}=\dfrac{7-2\sqrt{7}+1}{2}=4-\sqrt{7}\)
\(x_2=\dfrac{m+1}{6}=\dfrac{7-2\sqrt{7}+1}{6}=\dfrac{4-\sqrt{7}}{3}\)
Với \(m=7+2\sqrt{7}\) ta có:
\(x_1=\dfrac{m+1}{2}=\dfrac{7+2\sqrt{7}+1}{2}=4+\sqrt{7}\)
\(x_2=\dfrac{m+1}{6}=\dfrac{7+2\sqrt{7}+1}{6}=\dfrac{4+\sqrt{7}}{3}\)

Ta có : 3x2 – 2(m + 1)x + 3m – 5 = 0 (1)
(1) có hai nghiệm phân biệt khi Δ’ > 0
⇔ (m + 1)2 – 3.(3m – 5) > 0
⇔ m2 + 2m + 1 – 9m + 15 > 0
⇔ m2 – 7m + 16 > 0
⇔ (m – 7/2)2 + 15/4 > 0
Điều này luôn đúng với mọi m ∈ R hay phương trình (1) luôn có hai nghiệm phân biệt., gọi hai nghiệm đó là x1; x2
Khi đó theo định lý Vi–et ta có 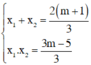 (I)
(I)
Phương trình có một nghiệm gấp ba nghiệm kia, giả sử x2 = 3.x1, khi thay vào (I) suy ra :
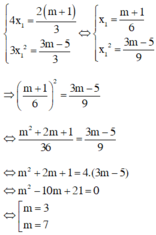
* TH1 : m = 3, pt (1) trở thành 3x2 – 8m + 4 = 0 có hai nghiệm x1 = 2/3 và x2 = 2 thỏa mãn điều kiện.
* TH2 : m = 7, pt (1) trở thành 3x2 – 16m + 16 = 0 có hai nghiệm x1 = 4/3 và x2 = 4 thỏa mãn điều kiện.
Kết luận : m = 3 thì pt có hai nghiệm là 2/3 và 2.
m = 7 thì pt có hai nghiệm 4/3 và 4.

Theo định lí Vi-ét: \(\hept{\begin{cases}x_1+x_2=\frac{2m+2}{3}\\x_1x_2=\frac{3m-5}{3}\end{cases}}\)
Ko mất tính tổng quát, giả sử \(x_1=3x_2\)
Có: \(\hept{\begin{cases}x_1=3x_2\\x_1+x_2=\frac{2m+2}{3}\end{cases}\Rightarrow}\hept{\begin{cases}x_1=\frac{m+1}{2}\\x_2=\frac{m+1}{6}\end{cases}}\)
Mà \(x_1x_2=\frac{3m-5}{3}\Rightarrow\frac{m+1}{2}.\frac{m+1}{6}=\frac{3m-5}{3}\)
\(\Leftrightarrow4\left(m+1\right)^2=3m-5\Leftrightarrow4m^2+5m+9=0\)(vô nghiệm)
Vậy ko tồn tại m thỏa mãn

Với m ≠ -1
Ta có: Δ = ( m - 3 ) 2 ≥ 0 , do đó phương trình luôn luôn có hai nghiệm x 1 , x 2
Lúc đó phương trình đã cho có hai nghiệm x = -1 và x = 4.

a.
\(f\left(x\right)=0\) có nghiệm \(x=1\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1-2\left(m-2\right)+m+10=0\)
\(\Rightarrow m=15\)
Khi đó nghiệm còn lại là: \(x_2=\dfrac{m+10}{x_1}=\dfrac{25}{1}=25\)
b.
Pt có nghiệm kép khi: \(\Delta'=\left(m-2\right)^2-\left(m+10\right)=0\)
\(\Rightarrow m^2-5m-6=0\Rightarrow\left[{}\begin{matrix}m=-1\\m=6\end{matrix}\right.\)
Với \(m=-1\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=-3\)
Với \(m=6\) nghiệm kép là: \(x=-\dfrac{b}{2a}=m-2=4\)
c.
Pt có 2 nghiệm âm pb khi:
\(\left\{{}\begin{matrix}\Delta'=m^2-5m-6>0\\x_1+x_2=2\left(m-2\right)< 0\\x_1x_2=m+10>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -1\\m>6\end{matrix}\right.\\m< 2\\m>-10\end{matrix}\right.\) \(\Rightarrow-10< m< -1\)
d.
\(f\left(x\right)< 0;\forall x\in R\Rightarrow\left\{{}\begin{matrix}a=1< 0\left(\text{vô lý}\right)\\\Delta'=m^2-5m-6< 0\end{matrix}\right.\)
Không tồn tại m thỏa mãn

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn


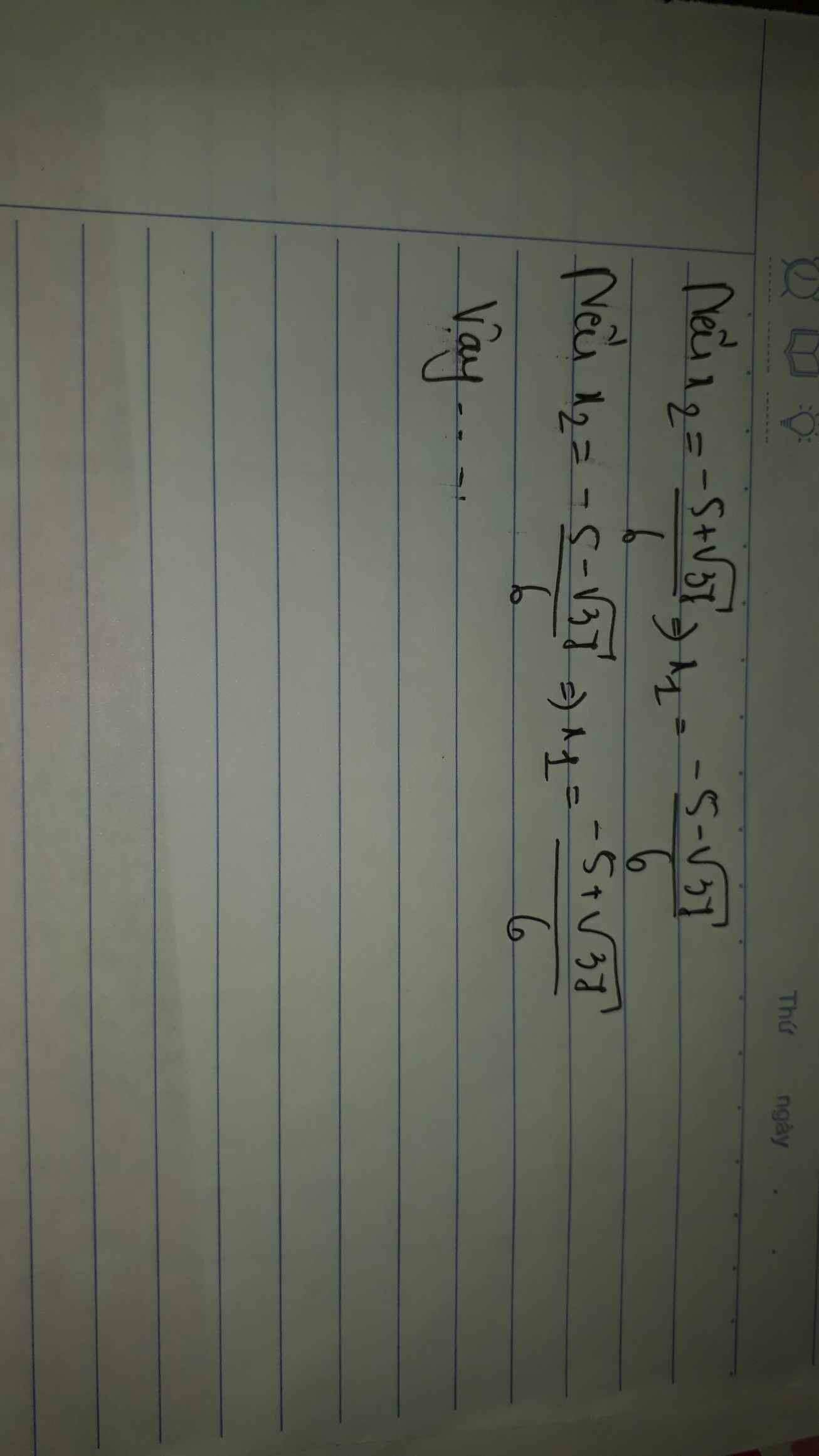
\(3x^2-2\left(m+1\right)x+3m-5=0\)
Xét \(\Delta=4\left(m+1\right)^2-4.3.\left(3m-5\right)\)\(=4m^2-28m+64=4\left(m-\dfrac{7}{2}\right)^2+15>0\forall m\)
=> pt luôn có hai nghiệm pb
Kết hợp viet và giả thiết có hệ: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+1\right)}{3}\\x_1=3x_2\\x_1x_2=\dfrac{3m-5}{3}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x_2+x_2=\dfrac{2m+2}{3}\\x_1=3x_2\\x_1x_2=\dfrac{3m-5}{3}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{6}\\x_1=\dfrac{m+1}{2}\\x_1x_2=\dfrac{3m-5}{3}\end{matrix}\right.\)
\(\Rightarrow\dfrac{\left(m+1\right)}{6}.\dfrac{\left(m+1\right)}{2}=\dfrac{3m-5}{3}\)\(\Leftrightarrow m^2-10m+21=0\) \(\Leftrightarrow\left[{}\begin{matrix}m=7\\m=3\end{matrix}\right.\)
Tại m=7 thay vào pt ta tìm được \(\left[{}\begin{matrix}x=4\\x=\dfrac{4}{3}\end{matrix}\right.\)
Tại m=3 thay vào pt ta tìm được \(\left[{}\begin{matrix}x=2\\x=\dfrac{2}{3}\end{matrix}\right.\)