Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1 :
Đk: \(x\ge1\)
\(\sqrt{x-1}+\sqrt{2x-1}=5\\ \Leftrightarrow x-1+2\sqrt{\left(x-1\right)\left(2x-1\right)}+2x-1=25\\ \Leftrightarrow2\sqrt{2x^2-3x+1}=27-3x\\ \)
\(\Leftrightarrow\begin{cases}27-3x\ge0\\4\left(2x^2-3x+1\right)=9x^2-162x+729\end{cases}\) \(\Leftrightarrow\begin{cases}x\le9\\x^2-150x+725=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x\le9\\x=145hoặcx=5\end{cases}\)
với x= 5 thoản mãn điều kiện, x=145 loại
Vậy \(S=\left\{5\right\}\)

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!

a)\(\Delta'=\left[\frac{-2.\left(m-1\right)}{2}\right]^2-m^2=m^2-2m+1-m^2=-2m+1\)
b)Để PT có hai nghiệm phân biệt thì \(\Delta'=-2m+1>0\Rightarrow m<\frac{1}{2}\)
Để PT có nghiệm kép thì: \(\Delta'=-2m+1=0\Rightarrow m=\frac{1}{2}\)
Để PT vô nghiệm thì: \(\Delta'=-2m+1<0\Rightarrow m>\frac{1}{2}\)

a: =>x+3>0
hay x>-3
b: \(\Leftrightarrow-\left(x-2\right)^2\left(x+2\right)>0\)
=>x+2<0
hay x<-2
c: =>x+4>0
hay x>-4
d: =>-3<x<4
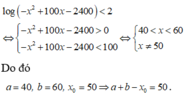
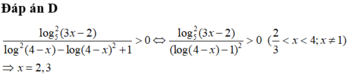
Đáp án là B