
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. ĐKXĐ: $x^2-16\neq 0\Leftrightarrow (x-4)(x+4)\neq 0$
$\Leftrightarrow x\neq \pm 4$
b. $A=\frac{x^2+8x+16}{x^2-16}=\frac{(x+4)^2}{(x-4)(x+4)}=\frac{x+4}{x-4}$
c. $A=3\Leftrightarrow \frac{x+4}{x-4}=3$
$\Rightarrow x+4=3(x-4)$
$\Leftrightarrow -2x+16=0$
$\Leftrightarrow x=8$ (tm)
d.
$A=0\Leftrightarrow \frac{x+4}{x-4}=0\Leftrightarrow x+4=0\Leftrightarrow x=-4$
Mà theo ĐKXĐ thì $x\neq \pm 4$ nên không tồn tại $x$ để $A=0$

a: \(B=\dfrac{x^2-1-2x+3x+1}{x\left(x-1\right)}=\dfrac{x^2+x}{x\left(x-1\right)}=\dfrac{x+1}{x-1}\)
a) B = \(\dfrac{x+1}{x}-\dfrac{2}{x-1}+\dfrac{3x+1}{x\left(x-1\right)}\) (ĐK: \(x\ne0;1\))
= \(\dfrac{\left(x+1\right)\left(x-1\right)}{x\left(x-1\right)}-\dfrac{2x}{x\left(x-1\right)}+\dfrac{3x+1}{x\left(x-1\right)}\)
= \(\dfrac{x^2-1-2x+3x+1}{x\left(x-1\right)}=\dfrac{x^2+x}{x\left(x-1\right)}=\dfrac{x+1}{x-1}\)
b) \(\left|x\right|=1< =>\left[{}\begin{matrix}x=1\left(L\right)\\x=-1\left(C\right)\end{matrix}\right.\)
Thay x = -1 vào B, ta có:
\(\dfrac{-1+1}{-1-1}=0\)
c) B nguyên <=> \(\dfrac{x+1}{x-1}\) nguyên <=> \(1+\dfrac{2}{x-1}\) nguyên
<=> 2\(⋮x-1\)
<=> x-1 \(\in\left\{-2;-1;1;2\right\}\)
| x-1 | -2 | -1 | 1 | 2 |
| x | -1 | 0 | 2 | 3 |
| C | L | C | C |
KL: x \(\in\left\{-1;2;3\right\}\)

Đk: \(x\ne1;x\ne0\)
a) \(E=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\left[\dfrac{x+1}{x}+\dfrac{1}{x-1}+\dfrac{2-x^2}{x\left(x-1\right)}\right]\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}:\dfrac{\left(x+1\right)\left(x-1\right)+x+2-x^2}{x\left(x-1\right)}\)
\(=\dfrac{x\left(x+1\right)}{\left(x-1\right)^2}.\dfrac{x\left(x-1\right)}{x+1}\)
\(=\dfrac{x^2}{x-1}\)
b) \(E>1\Leftrightarrow\dfrac{x^2}{x-1}>1\) \(\Leftrightarrow\dfrac{x^2-x+1}{x-1}>0\) \(\Leftrightarrow x-1>0\)
( do \(x^2-x+1=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\) )
\(\Leftrightarrow x>1\)
Vậy để E>1 thì x>1
c) \(E=\dfrac{x^2}{x-1}=\dfrac{x^2-1+1}{x-1}=\dfrac{\left(x-1\right)\left(x+1\right)+1}{x-1}=x+1+\dfrac{1}{x-1}\)
\(E\in Z\Leftrightarrow x+1+\dfrac{1}{x-1}\in Z\) mà \(x\in Z\)
\(\Rightarrow x-1\inƯ\left(1\right)=\left\{-1;1\right\}\)
\(\Leftrightarrow x=0\left(ktm\right);x=2\left(tm\right)\)
Vậy \(x=2\) thì \(E\in Z\).

a,\(M=\left(\frac{4}{x-4}-\frac{4}{x+4}\right).\frac{x^2+8x+16}{32}\)
\(M=\left(\frac{4\left(x+4\right)-4\left(x-4\right)}{\left(x+4\right)\left(x-4\right)}\right).\frac{\left(x+4\right)^2}{32}\)
\(M=\frac{4x+16-4x+16}{\left(x+4\right)\left(x-4\right)}.\frac{\left(x+4\right)^2}{32}\)
\(M=\frac{32\left(x+4\right)^2}{32\left(x+4\right)\left(x-4\right)}=\frac{x+4}{x-4}\)
b,
Để M = \(\frac{1}{3}\)
\(\Rightarrow x-4=3x+12\)
\(\Rightarrow2x=16\Leftrightarrow x=8\)
\(c,\)\(\frac{x+4}{x-4}=\frac{x-4+8}{x-4}\)
\(\Rightarrow x-4\inƯ\left(8\right)=\left(1;-1;2;-2;4;-4;8;-8\right)\)
\(\Rightarrow x-4\in\left(5;3;6;2;8;0;12;-4\right)\)
Vậy để M thuộc Z thì x phải thỏa mãn các điều kiện trên .

a: ĐKXĐ: x<>-2
b: \(A=\dfrac{\left(x+2\right)^2}{x+2}=x+2\)
c: Khi x=3 thì A=3+2=55
Khi x=-2 thì A ko xác định
d: Để A=2 thì x+2=2
=>x=0
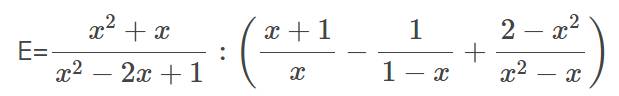
phân thức xác định khi và chỉ khi x khác 4.
\(B=\frac{x^2-8x+16}{x-4}\)
\(=\frac{\left(x-4\right)^2}{x-4}\)
\(=x-4\)
Để B=1 => x-4 = 1
<=>x=5 (thỏa mãn)
Vậy B=1 khi và chỉ khi x=5.
PHÂN thức