Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Theo bài ra ta có:
$x=\frac{3}{5}y$
$x+24=3y$
$\Rightarrow 24=3y-\frac{3}{5}y$
$\Rightarrow 24 = \frac{12}{5}y$
$\Rightarrow y=24.5:12=10$
$x=\frac{3}{5}.10=6$
Vậy phân số ban đầu là $\frac{6}{10}$

gọi a và b lần lượt là tử số và mẫu số của phân số ban đầu
nên ta có :\(\frac{a}{b}=\frac{5}{7}\)hay a.7=b.5
\(\Rightarrow\)\(\frac{a}{5}=\frac{b}{7}\)
Áp dụng định lí của dãy tỷ số bằng nhau ta có:
\(\frac{a}{5}=\frac{b}{7}=\frac{a+b}{5+7}=\frac{4812}{12}=401\)
Nếu \(\frac{a}{5}=401\)\(\Rightarrow a=401.5=2005\)
Nếu \(\frac{b}{7}=401\Rightarrow b=401.7=2807\)
Vậy phân số ban đầu là\(\frac{2005}{2807}\)

Tổng số phần bằng nhau là:
3 + 7 = 10 phần
Tử số là:
1100 : 10 x 3 = 330
Mẫu số là:
1100 - 330 = 770
Vậy phân số đó là \(\frac{330}{770}\)
Gọi a là tử, b là mẫu.
Ta có
\(\frac{a}{b}\)= \(\frac{3}{4}\)suy ra \(\frac{a}{3}\)= \(\frac{b}{4}\)
Áp dụng t/c dãy tỉ số = nhau ta có:
\(\frac{a}{3}\)= \(\frac{b}{4}\)= \(\frac{a+b}{3+4}\)= \(\frac{1100}{7}\)
\(\frac{a}{3}\)= \(\frac{1100}{7}\)nên a= \(\frac{3300}{7}\)=\(471\frac{3}{7}\)
\(\frac{b}{4}\)= \(\frac{1100}{7}\)nên b= \(\frac{4400}{7}\)=\(628\frac{4}{7}\)
vậy p/s đó là \(\frac{471\frac{3}{7}}{628\frac{4}{7}}\)

Gọi số tự nhiên cần tìm là n
Ta có: \(\frac{21}{32+n}=\frac{7}{15}\Leftrightarrow\frac{15.21}{7}=32+n\Leftrightarrow45=32+n\Leftrightarrow n=13\) 13
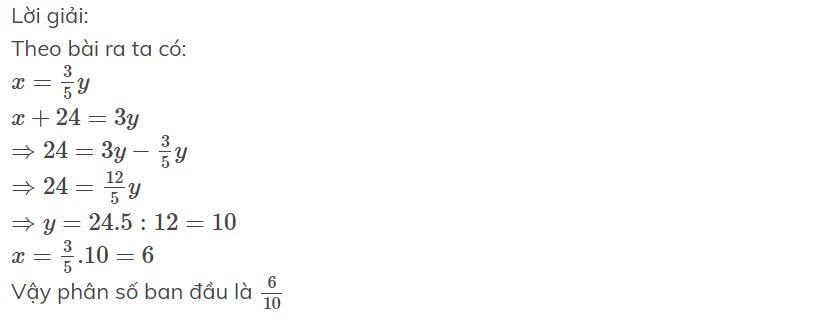
Ta có: \(\frac{x}{y}=\frac{3}{5}\); \(\frac{x+24}{y}\)=3 => \(\frac{x}{y}+\frac{24}{y}\) = 3
=> \(\frac{3}{5}+\frac{24}{y}=3\)
=> \(\frac{24}{y}=3-\frac{3}{5}\Rightarrow\frac{24}{y}=\frac{12}{5}\Rightarrow y=10\)
Khi y = 10, ta có:
\(\frac{x}{10}\)=\(\frac{3}{5}\) => x = \(\frac{10.3}{5}=6\)
Vậy phân số ban đầu là \(\frac{6}{10}\).