Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2 : đề bài này chỉ cần a,b>0 , ko cần phải thuộc N* đâu
a, Áp dụng bất đẳng thức AM-GM cho 2 số lhoong âm a,b ta được :
\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ba}}=2\) . Dấu "=" xảy ra khi a=b
b , Áp dụng BĐT AM-GM cho 2 số không âm ta được : \(a+b\ge2\sqrt{ab}\)
\(\dfrac{1}{a}+\dfrac{1}{b}\ge2\sqrt{\dfrac{1}{ab}}=\dfrac{2}{\sqrt{ab}}\)
Nhân vế với vế ta được :
\(\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge2.2.\dfrac{\sqrt{ab}}{\sqrt{ab}}=4\left(đpcm\right)\)
Dấu "="xảy ra tại a=b
Bài 1.
Vì a, b, c, d \(\in\) N*, ta có:
\(\dfrac{a}{a+b+c+d}< \dfrac{a}{a+b+c}< \dfrac{a}{a+b}\)
\(\dfrac{b}{a+b+c+d}< \dfrac{b}{a+b+d}< \dfrac{b}{a+b}\)
\(\dfrac{c}{a+b+c+d}< \dfrac{c}{b+c+d}< \dfrac{c}{c+d}\)
\(\dfrac{d}{a+b+c+d}< \dfrac{d}{a+c+d}< \dfrac{d}{c+d}\)
Do đó \(\dfrac{a}{a+b+c+d}+\dfrac{b}{a+b+c+d}+\dfrac{c}{a+b+c+d}+\dfrac{d}{a+b+c+d}< M< \left(\dfrac{a}{a+b}+\dfrac{b}{a+b}\right)+\left(\dfrac{c}{c+d}+\dfrac{d}{c+d}\right)\)hay 1<M<2.
Vậy M không có giá trị là số nguyên.

Giải:
Ta có:
\(\dfrac{a}{b}=\dfrac{-8}{11}\left(1\right)\Leftrightarrow1-\dfrac{a}{b}=1-\dfrac{-8}{11}\)
Hay \(\dfrac{b-a}{b}=\dfrac{11+8}{11}=\dfrac{19}{11}\left(2\right)\)
Thay \(b-a=190\) vào \(\left(2\right)\) ta được:
\(\dfrac{190}{b}=\dfrac{19}{11}\Leftrightarrow190.11=19b\Leftrightarrow b=110\)
Thay \(b=110\) vào \(\left(1\right)\) ta được:
\(\dfrac{a}{110}=\dfrac{-8}{11}\Leftrightarrow11a=-8.110\Leftrightarrow a=-80\)
Vậy phân số \(\dfrac{a}{b}\) cần tìm là \(\dfrac{-80}{110}\)
Thay b - a = 190 vào (1) ta được:
Phân số a/b phải tìm là -80/110

\(\dfrac{a}{b}=\dfrac{c}{d}\Leftrightarrow ad=bc\)
Ta có:
Nếu:
\(\dfrac{2a+c}{2b+d}=\dfrac{a-c}{b-d}\Leftrightarrow\left(2a+c\right)\left(b-d\right)=\left(a-c\right)\left(2b+d\right)\)
\(\Leftrightarrow2a\left(b-d\right)+c\left(b-d\right)=a\left(2b+d\right)-c\left(2b+d\right)\)
\(\Leftrightarrow2ab-2ad+bc-cd=2ab+ad-2bc+cd\)
\(\Leftrightarrow ad=bc\)
\(\Leftrightarrow\dfrac{2a+c}{2b+d}=\dfrac{a-c}{b-d}\left(đpcm\right)\)

a) Ta có : điều đề bài cho:\(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Leftrightarrow\)\(\dfrac{a}{b}+1=\dfrac{c}{d}+1\)
=)\(\dfrac{a}{b}+\dfrac{b}{b}=\dfrac{c}{d}+\dfrac{d}{d}\)
=)\(\dfrac{a+b}{b}=\dfrac{c+d}{d}\)(đpcm)
b) Điều đề bài cho:
\(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Leftrightarrow\)\(\dfrac{a}{b}-1=\dfrac{c}{d}-1\)
\(\Rightarrow\)\(\dfrac{a}{b}-\dfrac{b}{b}=\dfrac{c}{d}-\dfrac{d}{d}\)
\(\Rightarrow\)\(\dfrac{a-b}{b}=\dfrac{c-d}{d}\)(đpcm)

Giải
Ta có : \(\dfrac{1}{2^2}< \dfrac{1}{1.2};\dfrac{1}{3^2}< \dfrac{1}{2.3};\dfrac{1}{4^2}< \dfrac{1}{3.4};...;\dfrac{1}{20^2}< \dfrac{1}{19.20}\)
\(\Rightarrow\)D < \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{19.20}\)
Nhận xét: \(\dfrac{1}{1.2}=1-\dfrac{1}{2};\dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3};\dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4};...;\dfrac{1}{19.20}=\dfrac{1}{19}-\dfrac{1}{20}\)
\(\Rightarrow\) D< 1- \(\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{19}-\dfrac{1}{20}\)
D< 1 - \(\dfrac{1}{20}\)
D< \(\dfrac{19}{20}\)<1
\(\Rightarrow\)D< 1
Vậy D=\(\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{5^2}\)<1
A=\(\dfrac{1}{2^2}+\dfrac{1}{4^2}+\dfrac{1}{6^2}+...+\dfrac{1}{100^2}\)
A=\(\dfrac{1}{2^2.1}+\dfrac{1}{2^2.2^2}+\dfrac{1}{3^2.2^2}+...+\dfrac{1}{50^2.2^2}\)
A=\(\dfrac{1}{2^2}\left(1+\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{50^2}\right)\)
\(A=\dfrac{1}{2^2}\left(1+\dfrac{1}{2.2}+\dfrac{1}{3.3}+...+\dfrac{1}{50.50}\right)\)
Ta có :
\(\dfrac{1}{2.2}< \dfrac{1}{1.2};\dfrac{1}{3.3}< \dfrac{1}{2.3};\dfrac{1}{4.4}< \dfrac{1}{3.4};...;\dfrac{1}{50.50}< \dfrac{1}{49.50}\)
\(\Rightarrow A< \dfrac{1}{2^2}\left(1+\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{49.50}\right)\)Nhận xét :
\(\dfrac{1}{1.2}< 1-\dfrac{1}{2};\dfrac{1}{2.3}< \dfrac{1}{2}-\dfrac{1}{3};...;\dfrac{1}{49.50}< \dfrac{1}{49}-\dfrac{1}{50}\)
\(\Rightarrow A< \dfrac{1}{2^2}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{49}-\dfrac{1}{50}\right)\)
A<\(\dfrac{1}{2^2}\left(1-\dfrac{1}{50}\right)\)
A<\(\dfrac{1}{4}.\dfrac{49}{50}\)<1
A<\(\dfrac{49}{200}< \dfrac{1}{2}\)
\(\Rightarrow A< \dfrac{1}{2}\)

Tính các tổng dưới đây sau khi đã rút gọn phân số :
a)\(\dfrac{7}{21}\) + \(\dfrac{9}{-36}\) = \(\dfrac{7}{21}\)+\(\dfrac{-9}{36}\)=\(\dfrac{1}{3}\)+\(\dfrac{-1}{4}\)=\(\dfrac{4}{12}\)+\(\dfrac{-3}{12}\)=\(\dfrac{1}{12}\)
b) \(\dfrac{-12}{18}\)+\(\dfrac{-21}{35}\)=\(\dfrac{-2}{3}\)+\(\dfrac{-3}{5}\)=\(\dfrac{-10}{15}\)+\(\dfrac{-9}{15}\)=\(\dfrac{-19}{15}\)
c) \(\dfrac{-3}{21}\)+\(\dfrac{6}{42}\)=\(\dfrac{-1}{7}\)+\(\dfrac{1}{7}\)=0
d) \(\dfrac{-18}{24}\)+\(\dfrac{15}{-21}\)=\(\dfrac{-18}{24}\)+\(\dfrac{-15}{21}\)=\(\dfrac{-3}{4}\)+\(\dfrac{-5}{7}\)=\(\dfrac{-21}{28}\)+\(\dfrac{-20}{28}\)=\(\dfrac{-41}{28}\)
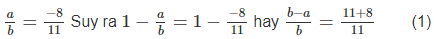
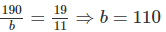
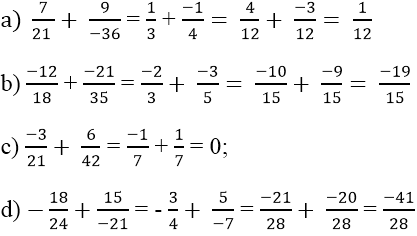
Theo đề bài ta có \(\dfrac{a}{b}=\dfrac{c}{d}\)
=> \(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a+c}{b+d}\) ( tính chất dãy tỉ số = nhau )
=> \(\dfrac{a}{b}=\dfrac{c}{d}=\dfrac{a-c}{b-d}\) ( tính chất dãy tỉ số = nhau )
Bạn giải thích rõ chỗ suy ra đc không