Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử \(a\ge b\Rightarrow a=b+m\left(m\ge0\right)\)
Ta có :
\(\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{b+m}{b}+\dfrac{b}{b+m}\) \(=1+\dfrac{m}{b}+\dfrac{b}{b+m}\ge1\) \(+\dfrac{m}{b+m}+\dfrac{b}{b+m}\)
\(=1+\dfrac{m+b}{b+m}=1+1=2\)
Dấu \("="\) chỉ xảy ra khi \(\left\{{}\begin{matrix}m=0\\a=b\end{matrix}\right.\)
Vậy \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\) \(\rightarrowđpcm\)
~ Chúc bn học tốt ~
Ta có : \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{a}{b}+\dfrac{b}{a}}\) ( theo bất đẳng thức Cô-si )
\(\Rightarrow\) \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\)

Bài 2 : đề bài này chỉ cần a,b>0 , ko cần phải thuộc N* đâu
a, Áp dụng bất đẳng thức AM-GM cho 2 số lhoong âm a,b ta được :
\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ba}}=2\) . Dấu "=" xảy ra khi a=b
b , Áp dụng BĐT AM-GM cho 2 số không âm ta được : \(a+b\ge2\sqrt{ab}\)
\(\dfrac{1}{a}+\dfrac{1}{b}\ge2\sqrt{\dfrac{1}{ab}}=\dfrac{2}{\sqrt{ab}}\)
Nhân vế với vế ta được :
\(\left(a+b\right)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)\ge2.2.\dfrac{\sqrt{ab}}{\sqrt{ab}}=4\left(đpcm\right)\)
Dấu "="xảy ra tại a=b
Bài 1.
Vì a, b, c, d \(\in\) N*, ta có:
\(\dfrac{a}{a+b+c+d}< \dfrac{a}{a+b+c}< \dfrac{a}{a+b}\)
\(\dfrac{b}{a+b+c+d}< \dfrac{b}{a+b+d}< \dfrac{b}{a+b}\)
\(\dfrac{c}{a+b+c+d}< \dfrac{c}{b+c+d}< \dfrac{c}{c+d}\)
\(\dfrac{d}{a+b+c+d}< \dfrac{d}{a+c+d}< \dfrac{d}{c+d}\)
Do đó \(\dfrac{a}{a+b+c+d}+\dfrac{b}{a+b+c+d}+\dfrac{c}{a+b+c+d}+\dfrac{d}{a+b+c+d}< M< \left(\dfrac{a}{a+b}+\dfrac{b}{a+b}\right)+\left(\dfrac{c}{c+d}+\dfrac{d}{c+d}\right)\)hay 1<M<2.
Vậy M không có giá trị là số nguyên.

a)Ta có:\(\dfrac{1}{b}-\dfrac{1}{b+1}=\dfrac{b+1-b}{b\left(b+1\right)}=\dfrac{1}{b^2+b}< \dfrac{1}{b^2}\)(do b>1)
\(\dfrac{1}{b-1}-\dfrac{1}{b}=\dfrac{b-b+1}{\left(b-1\right)b}=\dfrac{1}{b^2-b}>\dfrac{1}{b^2}\)(do b>1)
b)Áp dụng từ câu a
=>\(\dfrac{1}{2}-\dfrac{1}{3}< \dfrac{1}{2^2}< \dfrac{1}{1}-\dfrac{1}{2}\)
\(\dfrac{1}{3}-\dfrac{1}{4}< \dfrac{1}{3^2}< \dfrac{1}{2}-\dfrac{1}{3}\)
.........................
\(\dfrac{1}{9}-\dfrac{1}{10}< \dfrac{1}{9^2}< \dfrac{1}{8}-\dfrac{1}{9}\)
=>\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}< S< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{8}-\dfrac{1}{9}\)
=>\(\dfrac{1}{2}-\dfrac{1}{10}< S< 1-\dfrac{1}{9}\)
=>\(\dfrac{2}{5}< S< \dfrac{8}{9}\)(đpcm)

b)
\(B=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2016}}\\ 2B=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2015}}\\ 2B-B=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2015}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2016}}\right)\\ B=1-\dfrac{1}{2^{2016}}< 1\)
Vậy B < 1 (đpcm)

Ta có :
\(A=\dfrac{1}{1.300}+\dfrac{1}{2.301}+\dfrac{1}{3.302}+.............+\dfrac{1}{101.400}\)
\(299A=\dfrac{299}{1.300}+\dfrac{299}{2.301}+\dfrac{299}{3.302}+...................+\dfrac{299}{101.400}\)
\(299A=1-\dfrac{1}{300}+\dfrac{1}{2}-\dfrac{1}{301}+..............+\dfrac{1}{101}-\dfrac{1}{400}\)
\(299A=\left(1+\dfrac{1}{2}+................+\dfrac{1}{101}\right)-\left(\dfrac{1}{300}+\dfrac{1}{301}+..............+\dfrac{1}{400}\right)=C\)
\(\Rightarrow A=\dfrac{C}{299}\)
Lại có :
\(B=\dfrac{1}{1.102}+\dfrac{1}{2.103}+\dfrac{1}{3.104}+................+\dfrac{1}{299.400}\)
\(101B=\dfrac{101}{1.102}+\dfrac{101}{2.103}+\dfrac{101}{3.104}+...............+\dfrac{101}{299.400}\)
\(101B=1-\dfrac{1}{102}+\dfrac{1}{2}-\dfrac{1}{103}+..................+\dfrac{1}{299}-\dfrac{1}{400}\)
\(101B=\left(1+\dfrac{1}{2}+..............+\dfrac{1}{299}\right)-\left(\dfrac{1}{102}-\dfrac{1}{103}+...............+\dfrac{1}{400}\right)=C\)
\(\Rightarrow B=\dfrac{C}{101}\)
\(\Rightarrow\dfrac{A}{B}=\dfrac{C}{101}:\dfrac{C}{299}=\dfrac{101}{299}\)
~ Chúc bn học tốt ~

a) (1/7.x-2/7).(-1/5.x-2/5)=0
=> 1/7.x-2/7=0hoặc-1/5.x-2/5=0
*1/7.x-2/7=0
1/7.x=0+2/7
1/7.x=2/7
x=2/7:1/7
x=2
b)1/6.x+1/10.x-4/5.x+1=0
(1/6+1/10-4/5).x+1=0
(1/6+1/10-4/5).x=0-1
(1/6+1/10-4/5).x=-1
(-8/15).x=-1
x=-1:(-8/15) =15/8

Ta có : \(\frac{a}{b}+\frac{b}{a}-2\)
\(=\frac{a^2}{ab}+\frac{b^2}{ab}-\frac{2ab}{ab}\)
\(=\frac{a^2-2ab+b^2}{ab}\)
\(=\frac{\left(a-b\right)^2}{ab}\ge0\) ( do a;b > 0 )
Dấu "=" xảy ra khi :
\(a-b=0\Leftrightarrow a=b\)
Vậy ...
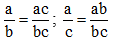
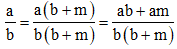
Giải:
Không giảm tính tổng quát
Giả sử \(a\ge b\Rightarrow a=b+m\left(m\ge0\right)\)
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{b+m}{b}+\dfrac{b}{b+m}\)
\(=1+\dfrac{m}{b}+\dfrac{b}{b+m}\ge1+\dfrac{m}{b+m}+\dfrac{b}{b+m}\)
\(=1+\dfrac{m+b}{b+m}=1+1=2\)
Dấu "=" xảy ra khi \(\Leftrightarrow\left\{{}\begin{matrix}m=0\\a=b\end{matrix}\right.\)
Vậy \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\) (Đpcm)
Thanks