Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Thay m=2 vào (d), ta được:
y=2x-2+1=2x-1
Phương trình hoành độ giao điểm là:
\(x^2=2x-1\)
=>\(x^2-2x+1=0\)
=>(x-1)^2=0
=>x-1=0
=>x=1
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Vậy: Khi m=2 thì (P) cắt (d) tại A(1;1)
b: Phương trình hoành độ giao điểm là:
\(x^2=2x-m+1\)
=>\(x^2-2x+m-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(m-1\right)\)
=4-4m+4
=-4m+8
Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0
=>-4m+8>0
=>-4m>-8
=>m<2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
y1,y2 thỏa mãn gì vậy bạn?

a) pt hoành độ giao điểm: \(x^2-2x+3-m^2=0\)
Để đường thẳng d cắt (P) tại 2 điểm phân biệt thì \(\Delta'>0\)
\(\Delta'=1+m^2-3\Rightarrow m^2-2>0\Rightarrow\left|m\right|>\sqrt{2}\)
b) Gọi giao điểm là \(A\left(x_1,y_1\right);B\left(x_2,y_2\right)\)
\(\Rightarrow A\left(x_1,x_1^2\right);B\left(x_2,x_2^2\right)\)
Áp dụng hệ thức Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=3-m^2\end{matrix}\right.\)
Theo đề: \(y_1-y_2=8\Rightarrow x_1^2-x_2^2=8\Rightarrow\left(x_1-x_2\right)\left(x_1+x_2\right)=8\)
\(\Rightarrow x_1-x_2=4>0\)
Ta có: \(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2=4m^2-8\)
\(\Rightarrow x_1-x_2=\sqrt{4m^2-8}\left(x_1-x_2>0\right)\Rightarrow4=\sqrt{4m^2-8}\)
\(\Rightarrow4m^2-8=16\Rightarrow m=\pm\sqrt{6}\)

Hoành độ của 2 giao điểm là nghiệm của phương trình
x2=mx+m+1x2=mx+m+1
⇒x2−mx−m−1=0⇒x2-mx-m-1=0
Δ=(−m)2+4(m+1)=m2+4m+4=(m+2)2≥0∀mΔ=(-m)2+4(m+1)=m2+4m+4=(m+2)2≥0∀m
Vậy phương trình luôn có nghiệm
Để (P)(P) cắt (d)(d) tại 2 điểm có hoành độ x1x1 và x2x2 thì
Δ>0Δ>0
⇒m≠2⇒m≠2
Để 2 giao điểm khác phía với trục tung thì
x1.x2<0x1.x2<0
Theo hệ thức vi-ét
⇒⇒{x1.x2=−m−1x1+x2=m{x1.x2=−m−1x1+x2=m
Để −m−1<0-m-1<0
⇒m≻1⇒m≻1
Ta lại có
{x1+x2=m2x2−3x2=5{x1+x2=m2x2−3x2=5
⇒{2x1+2x2=2m2x1−3x2=5⇒{2x1+2x2=2m2x1−3x2=5
⇒{x1+x2=m5x2=2m−5⇒{x1+x2=m5x2=2m−5
⇒{x1+x2=mx2=2m−55⇒{x1+x2=mx2=2m−55
⇒⎧⎪ ⎪⎨⎪ ⎪⎩x1=5m−2m+55=3m+55x2=2m−55⇒{x1=5m−2m+55=3m+55x2=2m−55
Thay x1x1 và x2x2 vào
x1.x2=−m−1x1.x2=-m-1
Ta được
3m+55.2m−55=−m−13m+55.2m-55=-m-1
⇒6m2−5m−25=−25m−25⇒6m2-5m-25=-25m-25
⇒6m2+20m=0⇒6m2+20m=0
⇒2m(3m+10)=0⇒2m(3m+10)=0
⇒⇒⎡⎣m=0(TM)m=−103(KTM)[m=0(TM)m=−103(KTM)
Vậy với m=0m=0 thì thõa mãn đầu bài
Sai dấu làm dò mãi mới ra

Phương trình hoành độ giao điểm:
\(x^2=2x-m+9\Leftrightarrow x^2-2x+m-9=0\) (1)
(d) cắt (P) tại 2 điểm nằm về 2 phía trục tung
\(\Leftrightarrow\) (1) có 2 nghiệm pb trái dấu
\(\Leftrightarrow ac< 0\Leftrightarrow m-9< 0\Rightarrow m< 9\)

- xét phương trình hoành độ giao điểm : \(x^2=\left(2m-1\right)x-m+2\)\(\Leftrightarrow x^2-\left(2m-1\right)x+m-2=0\)có \(\Delta=\left(2m-1\right)^2-4\left(m-2\right)=4m^2-8m+9=\left(2m-1\right)^2+8\ge8\)vậy nên phương trinh luôn có 2 nghiệm phân biệt tức hai đồ thị luôn cắt nhau tại 2 điểm phân biệt A và B
- Có viet : \(\hept{\begin{cases}x_1+x_2=2m-1\\x_1x_2=m-2\end{cases}}\)ta có : \(A\left(x_1,y_1\right)=A\left(x_1,x_1^2\right)\)và \(B\left(x_2,y_2\right)=B\left(x_2,x_2^2\right)\)
nên ta có : \(x_1y_1+x_2y_2=0\Leftrightarrow x_1^3+x_2^3=0\)\(\Leftrightarrow\left(x_1+x_2\right)\left(\left(x_1+x_2\right)^2-3x_1x_2\right)=0\)\(\Leftrightarrow\left(2m-1\right)\left[\left(2m-1\right)^2-3m+6\right]=0\)
- \(2m-1=0\Leftrightarrow m=\frac{1}{2}\)
- \(\left(2m-1\right)^2-3m+6=0\Leftrightarrow4m^2-7m-7=0\)VN
2. Cho parabol (P): y = x2 và đường thẳng (d): y = 2(m – 1)x + m2 + 2m (m là tham số, m ∈ R )
a) Chứng minh rằng đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt A, B?
b) Gọi H và K lần lượt là hình chiếu của A và B trên trục hoành.
Tìm m sao cho: OH2 + OK2 = 6 mọi người hướng dẫ mk ý b vs
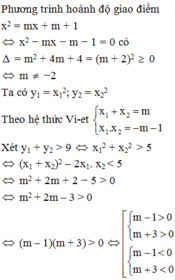
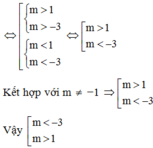
đường thẳng \(d^'\)và \(d\)cắt nhau tại một điểm A trên trục tung nên điểm A có hoành độ \(x_a=0\)và tạo độ A thỏa mãn phương trình \(d^'\)nên :\(\Rightarrow y_a=-2.0+1=1\)\(\Rightarrow A\left(0;1\right)\)Mà do a là giao điểm của 2 đường \(d;d^'\)nên toạn độ A cũng thỏa mãn phương trình của \(d\): \(\Rightarrow1=-m^2+m+1\Leftrightarrow m^2-m=0\Leftrightarrow m\left(m-1\right)=0\Leftrightarrow m\orbr{\begin{cases}m=0\\m=1\end{cases}}\)
câu b :
Xét phương trình hoành độ gia điểm của P và d có :
\(x^2=2mx-m^2+m+1\Leftrightarrow x^2-2mx+m^2-m-1=0\)
để hai đồ thị cắt nhau tại 2 điểm phân biệt thì \(\Delta^'=m^2+m^2-m-1=2m^2-m-1>0\)
\(\left(m-1\right)\left(2m+1\right)>0\Leftrightarrow\orbr{\begin{cases}m< -\frac{1}{2}\\m>1\end{cases}}@\)
khi đó theo vieet có :\(\hept{\begin{cases}x_1+x_2=2m\\x_1x_2=-m^2+m+1\end{cases}}\)
\(\Rightarrow y_1+y_2+2\left(x_1+x_2\right)=22\)với \(y_1=x^2_1;y_2=x_2^2\)
\(\Rightarrow\left(\left(x_1+x_2\right)^2-2x_1.x_2\right)+\left(x_1+x_2\right)2=22\)thay vieet ta có :
\(\left(2m\right)^2-2\left(-m^2+m+1\right)+2.2m=22\)
\(\Leftrightarrow6m^2+2m-24=0\Leftrightarrow\orbr{\begin{cases}m=\frac{-1+\sqrt{144}}{6}\\m=\frac{-1-\sqrt{144}}{6}\end{cases}}\)thỏa mãn @
Kết luận nghiệm
tính denta sai rùi rùi bạn ơi
phải là 145 chứ ko phải 144