Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D.
Hoành độ giao điểm hai đồ thị là nghiệm của phương trình:
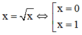
Thể tích cần tính:
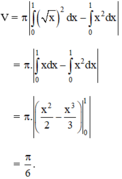

Chọn D
D quay xung quanh trục Oy
Ta có: y = ( x - 2 ) 2 ⇔ x - 2 = ± y ⇔ x = 2 ± y
V = π ∫ 0 4 2 + y 2 - 2 - y 2 dy = 8 π . ∫ 0 4 y dy = 8 π . 2 3 y 3 2 | 0 π = 128 π 3 đ v t t

Đáp án: D.
Hướng dẫn: Thể tích khối tròn xoay này được tính bởi
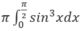

Đáp án D
Phương pháp:
Công thức tính thể tích hình phẳng được giới hạn bởi các đường thẳng x = a , x = b ( a < b ) và các đồ thị hàm số ư
y = f(x), y = g(x) khi quay quanh trục Ox là: V = π ∫ a b f 2 x - g 2 x dx
Cách giải:
Ta có công thức tính thể tích hình phẳng đã cho là:
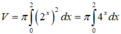
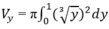
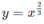 , x = 0 và tiếp tuyến với đường
, x = 0 và tiếp tuyến với đường 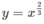 tại điểm có hoành độ x = 1, quanh trục Oy;
tại điểm có hoành độ x = 1, quanh trục Oy;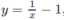 , y = 0, y = 2x, quanh trục Ox
, y = 0, y = 2x, quanh trục Ox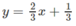
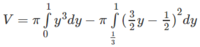
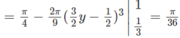
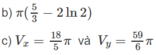
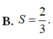
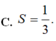
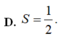

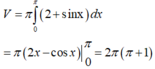
Chọn C.
Tiếp tuyến (d) qua O có dạng y = kx, k > 0. (d) tiếp xúc với (P) tại điểm có hoành độ x 0
khi hệ x 0 2 + m = k x 0 2 x 0 = k > 0 có nghiệm x 0 tức là phương trình x 0 2 = m có nghiệm x 0 > 0 h a y
x 0 = m v à m ≥ 0 suy ra k = 2 m
Phương trình (d): y = 2 m x
Mà V = 6 π suy ra m = ± 6 mà m ≥ 0 suy ra m = 6
Vậy m = 6 thỏa mãn bài toán.