Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hoành độ giao điểm (P) ; (d) tm pt
\(\frac{1}{2}x^2+mx+m-1=0\Leftrightarrow x^2+2mx+2m-2=0\)
\(\Delta'=m^2-\left(2m-2\right)=m^2+2m+2=\left(m+1\right)^2+1>0\)
Vậy (P) cắt (d) tại 2 điểm pb

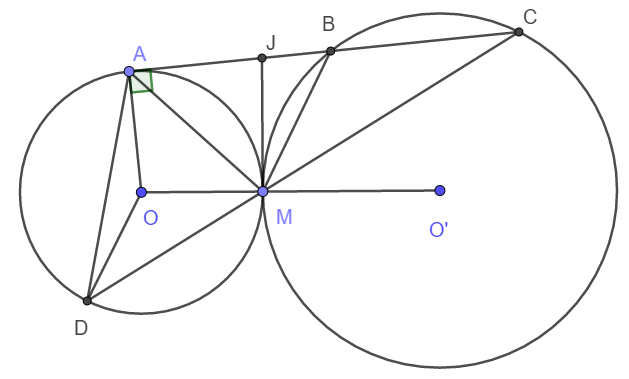
a) Từ M, kẻ \(MJ\perp OO'\left(J\in AC\right)\)
Khi đó ta có \(\widehat{BMA}=\widehat{BMJ}+\widehat{JMA}=\widehat{BCM}+\widehat{ADM}\)
\(=\frac{\widebat{AD}-\widebat{AM}}{2}+\frac{\widebat{AM}}{2}=\frac{\widebat{AD}}{2}=\widehat{AMD}\)
Vậy MA là tia phân giác góc \(\widehat{BMD}\)
b) Xét tam giác AMB và DMA có:
\(\widehat{BAM}=\widehat{ADM}\left(=\frac{\widebat{AM}}{2}\right)\)
\(\widehat{AMB}=\widehat{DMA}\left(cma\right)\)
\(\Rightarrow\Delta AMB\sim\Delta DMA\left(g-g\right)\)
\(\Rightarrow\frac{AM}{MD}=\frac{MB}{AM}\Rightarrow AM^2=MD.MB\)

Tr oii câu này ra lâu lắm rồi mà chả có ai trả lời. Chắc bây giờ bn í tầm 17 tuổi r ^_^


tk ủng hộ đi