Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
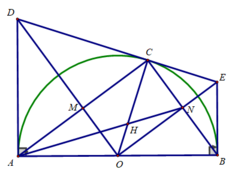
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật
a) Nối B với M
Xét tam giác OBM,có:
OB=OM(Cùng là bán kính)
=>Tam giác OBM cân tại O
=>Góc OMB=Góc OBM (2gocs tương ứng)
Ta có:By tiếp tuyến với đg tròn (O) tại B
=>Góc OBy=90o(t/c...)
Hay góc OBC=90o (C∈By)
CD tiếp tuyến với đg tròn (O)
=>Góc OMD=góc OMC=90o(t/c...)
Ta có:OBM+MBD=OBD
OMB+BMD=OMD
MàOBM=OMB (cmt)
OBD=OMD (=90o)
=>MBD=BMD
Xét tam giác BMD, có:
MBD=BMD (cmt)
=>Tam giác BMD cân tại D
=>BD=MD (2 cạnh tương ứng)
Nối A với M
Xét tam giác AOM,có:
OA=OM (cùng là R)
=>TAm giác OAM cân tại O
=>OAM=OMA(2 góc tương ứng)
Ta có :Ax tiếp tuyến với đg tròn (O) tại A
=>OAx=90o
HayOAC=90o (C∈Ax)
Ta có :OAM+MAC=OAC
OMA+AMC=OMC
Mà:OAM=OMA(cmt)
OAC=OMC(=90o)
=>MAC=AMC
Xét tam giác ACM,có:
MAC=AMC(cmt)
=>Tam giác ACM cân tại C
=>AC=CM(2 cạnh tương ứng)
Ta có:CM+MD=CD
Mà:CM=AC(cmt)
MD=BD(cmt)
=>AC+BD=CD
b)Gọi E là gđ của AM và CO
Ta có : AC cắt CM tại C
Mà AC và CM là tiếp tuyến của đg tròn (O)
=>AC=MC;CO là p/g của ACM(...)
Vì CO là p/g của ACM(cmt)
=>ACO=MCO
Hay ACI=MCI
Xét tam giác ACI và tam giác MCI,có:
AC=MC(cmt)
ACO=MCO(cmt)
CI là cạnh chung
=>Tam giác ACI=Tam giác MCI(c.g.c)
=>AIC=MIC(2 góc tương ứng);AI=MI
Ta có:AIC+MIC=180o(2 góc bù nhau)
Mà AIC=MIC(cmt)
=>AIC=90o
=>OC⊥AM tại I
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE
C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân
