K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

23 tháng 6 2023
a: góc AMC=góc AHC=90 độ
=>AMHC nội tiếp
b: Đề sai rồi bạn

12 tháng 5 2023
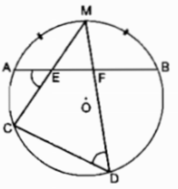
a: góc AEB=1/2*180=90 độ
góc FIB+góc FEB=180 độ
=>FIBE nội tiếp
b: góc ACB=1/2*180=90 độ
=>AC vuông góc DB
Xét ΔCAF và ΔCEA có
góc CAF=góc CEA
góc ACF chung
=>ΔCAF đồng dạng với ΔCEA
=>CA^2=AF*AE
Xét ΔDAB vuông tại D có AC vuông góc DB
nên CA^2=CD*CB=AF*AE

P là điểm chính giữa của cung nhỏ AB
=>\(sđ\stackrel\frown{PA}=sđ\stackrel\frown{PB}\)
Xét (O) có
\(\widehat{ADP}\) là góc nội tiếp chắn cung AP
\(\widehat{BAP}\) là góc nội tiếp chắn cung PB
\(sđ\stackrel\frown{PA}=sđ\stackrel\frown{PB}\)
Do đó: \(\widehat{ADP}=\widehat{BAP}\)
Trên nửa mặt phẳng bờ AB có chứa điểm P, kẻ tia Ax là tiếp tuyến của đường tròn ngoại tiếp ΔACD
Khi đó, ta sẽ có:
\(\widehat{xAC}\) là góc tạo bởi tiếp tuyến Ax và dây cung AC của đường tròn ngoại tiếp ΔACD
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC của đường tròn ngoại tiếp ΔACD
Do đó: \(\widehat{xAC}=\widehat{ADC}\)
mà \(\widehat{ADP}=\widehat{ADC}=\widehat{BAP}\)
nên \(\widehat{xAC}=\widehat{BAP}\)
=>\(\widehat{xAC}=\widehat{CAP}\)
=>Ax và AP là hai tia trùng nhau
=>PA là tiếp tuyến của (ACD)