Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

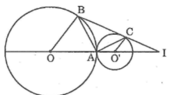
Ta có : OB // O’C (gt)
Suy ra : (hai góc trong cùng phía)
OA = OB (=R)
⇒ Tam giác AOB cân tại O

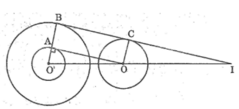
Xét tứ giác ABCO ta có:
AB // CO (gt) (1)
Mà : AB = O’B – O’A = 3 – 1 = 2 (cm)
Suy ra: AB = OC = 2 (cm) (2)
Từ (1) và (2) suy ra: ABCO là hình bình hành
Lại có: OA ⊥ O’A (tính chất tiếp tuyến)
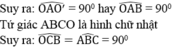
Suy ra: BC ⊥ OC và BC ⊥ O’B
Vậy BC là tiếp tuyến chung của hai đường tròn (O) và (O’)

O' O B C K Y A
a) Ta thấy ngay AY chính là tiếp tuyến chung của hai đường tròn (O) và (O')
Theo tính chất hai tiếp tuyến cắt nhau, ta có YB = YA = YC
Vậy nên tam giác BAC vuông tại A hay \(\widehat{BAC}=90^o\)
b) Theo tính chất hai tiếp tuyến cắt nhau ta có \(\widehat{AYO}=\widehat{OYB};\widehat{AYO'}=\widehat{O'YC}\)
\(\Rightarrow\widehat{OYO'}=\widehat{OYA}+\widehat{AYO'}=90^o\)
Xét tam giác vuông OYO' có YK là trung tuyến ứng với cạnh huyền nên \(KY=\frac{OO'}{2}\)
c) Ta thấy ngay BOO'C là hình thang vuông có Y là trung điểm BC, K là trung điểm OO' nên KY là đường trung bình của hình thang.
Vậy thì KY // OB // O'C
Từ đó ta có ngay KY vuông góc BC.
Lại có \(KY=KO\)
Nên BC là tiếp tuyến của đường tròn tâm K, bán kính KO.



