Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAM vuông tại A có sin AMO=AO/OM=1/2
nên góc AMO=30 độ
b: Xét ΔOBM có
OA vừa là đường cao, vừa là trung tuyến
=>ΔOBM cân tại O
=>OB=OM=8cm

Δ
a: Xét ΔOAM vuông tại A có cos AOM=OA/OM=1/2
nên góc AOM=60 độ
=>góc AMO=30 độ
Xét ΔOAC có OA=OC và góc AOM=60 độ
nên ΔAOC đều
mà AH là đường cao
nên H là trung điểm của OC
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
Xét tứ giác OACB có
H là trung điểm chung của OC và BA
OA=OB
Do đó: OACB là hình thoi
b: góc DAM=180 độ-góc HAM=180-60=120 độ
góc DAO=180-60=120 độ
góc OAM=360-120-120=120 độ
=>góc DAM=góc DAO=góc OAM
=>ΔODM đều
=>MO=MD
=>M nằm trên trung trực của OD
mà NK là trung trực của OD
nên M,N,K thẳng hàng

a: Xét ΔOAM vuông tại A có cos AOM=OA/OM=1/2
nên góc AOM=60 độ
=>góc AMO=30 độ
Xét ΔOAC có OA=OC và góc AOM=60 độ
nên ΔAOC đều
mà AH là đường cao
nên H là trung điểm của OC
ΔOAB cân tại O
mà OH là đường cao
nên H là trung điểm của AB
Xét tứ giác OACB có
H là trung điểm chung của OC và BA
OA=OB
Do đó: OACB là hình thoi
b: góc DAM=180 độ-góc HAM=180-60=120 độ
góc DAO=180-60=120 độ
góc OAM=360-120-120=120 độ
=>góc DAM=góc DAO=góc OAM
=>ΔODM đều
=>MO=MD
=>M nằm trên trung trực của OD
mà NK là trung trực của OD
nên M,N,K thẳng hàng

1: Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: MA=MB
hay M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
nên O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO\(\perp\)AB
Gọi G là giao điểm của OM và AB
=>MO vuông góc với AB tại G
\(AM=R\sqrt{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}OG=\dfrac{R^2}{2R}=\dfrac{R}{2}\\GM=2R-\dfrac{R}{2}=\dfrac{3}{2}R\end{matrix}\right.\)
\(\Leftrightarrow AG=\dfrac{R^2\sqrt{3}}{2R}=\dfrac{R\sqrt{3}}{2}\)
\(\left\{{}\begin{matrix}S_{AGM}=S_{BGM}=\dfrac{AG\cdot GM}{2}=\dfrac{R\sqrt{3}}{2}\cdot\dfrac{3R}{2}:2=\dfrac{3R^2\sqrt{3}}{8}\\S_{OGA}=S_{OGB}=\dfrac{OG\cdot GB}{2}=\dfrac{R}{2}\cdot\dfrac{R\sqrt{3}}{2}:2=\dfrac{R^2\sqrt{3}}{8}\end{matrix}\right.\)
\(S_{AOBM}=2\cdot\left(S_{AGM}+S_{OGA}\right)=2\cdot\dfrac{4R^2\sqrt{3}}{8}=R^2\sqrt{3}\)
2: Xét tứ giác NHBI có
\(\widehat{NHB}+\widehat{NIB}=180^0\)
Do đó: NHBI là tứ giác nội tiếp
Suy ra: \(\widehat{NHI}=\widehat{NBA}\)
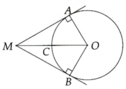
a: Xét ΔOAM vuông tại A có sin AMO=AO/OM=1/2
nên góc AMO=30 độ
b: Xét ΔOBM có
OA vừa là đường cao, vừa là trung tuyến
=>ΔOBM cân tại O
=>OB=OM=8cm