Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) tứ giác ABOC là hình vuông
vì BAC = 90 (giả thiết)
ABO = 90 (AB là tiếp tuyến)
ACO = 90 (AC là tiếp tuyến)
AB = AC (tính chất 2 tiếp tuyến cắt nhau)
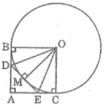
Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2.2 = 4 (cm)
Áp dụng đlí Py - ta - go cho tam giác BAO vuông tại B , ta có :
\(OA^2=OB^2+AB^2\)
\(AB^2=OA^2-OB^2=5^2-3^2=16\)
\(AB^2=16\Rightarrow AB=4cm\)
=> AC = 4cm
Theo tính chất 2tt cắt nhau , ta có :
DB = DM ; EC = EM
=> AD + DE + AE = AB + AC = 4 + 4 = 8
Vậy : chu vi tam giác ADE là : 8cm
Cho sửa câu c) thành tính góc DOE (:
a) Ta có :
\(AB\perp AC=>\widehat{BAC}=90^o\)
\(AB\perp BO=>\widehat{ABO}=90^o\)
\(AC\perp CO=>\widehat{ACO}=90^o\)
Tứ giác ABOC có 3 góc vuông nên nó là hình chữ nhật
Mặt khác : AB = AC (tính chất hai tiếp tuyến cắt nhau)
Suy ra tứ giác ABOC là hình vuông
b. Theo tính chất của hai tiếp tuyến cắt nhau ta có :
DB = DM
EM = EC
Chu vi của tam giác ADE bằng :
AD + DE + EA = AD + DM + ME + EA
= AD + DB + AE + EC = AB + AC = 2AB
Mà tứ giác ABOC là hình vuông (chứng minh trên) nên:
AB = OB = 2 (cm)
Vậy chu vi của tam giác ADE bằng: 2 . 2 = 4 (cm)
c. Theo tính chất của hai tiếp tuyến cắt nhau ta có:
OD là tia phân giác của góc BOM
\(\Rightarrow\widehat{BOD}=\widehat{DOM}=\frac{1}{2}\widehat{BOM}\)
OE là tia phân giác của góc COM
\(\Rightarrow\widehat{COE}=\widehat{EOM}=\frac{1}{2}\widehat{COM}\)
\(\Rightarrow\widehat{DOE}=\widehat{DOM}+\widehat{EOM}=\frac{1}{2}\left(\widehat{BOM}+\widehat{COM}\right)\)
\(=\frac{1}{2}\widehat{COB}=\frac{1}{2}.90^o=45^o\)
Áp dụng định lí Pitago vào tam giác vuông ABO, ta có:
A O 2 = A B 2 + B O 2
Suy ra: A B 2 = A O 2 - B O 2 = 5 2 - 3 2 = 16
AB = 4 (cm)
Theo tính chất của hai tiếp tuyến cắt nhau ta có:
DB = DM
EM = EC
Chu vi của tam giác ADE bằng:
AD + DE + EA = AD + DB + AE + EC
= AB + AC = 2AB = 2.4 = 8 (cm)
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=180^0\)
=>OBAC là tứ giác nội tiếp
b: Xét (O) có
DB,DM là tiếp tuyến
=>DB=DM và OD là phân giác của \(\widehat{BOM}\left(1\right)\)
Xét (O) có
EM,EC là tiếp tuyến
=>EM=EC và OE là phân giác của \(\widehat{MOC}\left(2\right)\)
\(C_{ADE}=AD+DE+AE\)
\(=AB-BD+DM+ME+AC-CE\)
\(=AB+AC=2AB\)
c: \(\widehat{DOE}=\widehat{DOM}+\widehat{EOM}\)
\(=\dfrac{1}{2}\left(\widehat{BOM}+\widehat{COM}\right)=\dfrac{1}{2}\cdot\widehat{BOC}\)
a) ta có : AB = AC (tính chất tiếp tuyến)
\(\Rightarrow\) tam giác ABC cân tại A
có OA là tia phân giác của góc A
\(\Rightarrow\) OA \(\perp\) BC \(\Rightarrow\) tam giác ABO vuông tại B có đường cao BH
ta có : OB2 = OA.OH \(\Leftrightarrow\) 32 = 5OH
\(\Rightarrow\) OH = \(\dfrac{9}{5}\) = 1,8 (cm)
