Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Giải
- Diện tích tam giác OBC là:
- (14+10+18) : 2+1=22 cm2

Trong hình chữ nhật ABCD gọi chiều cao ứng với các tam giác OAB,OBC,ODC,OAD lần lượt là \(h_1,h_2,h_3,h_4\)
Với mọi \(O\in ABCD\)có \(S_{OAB}+S_{ODC}=\frac{AB.h_1}{2}+\frac{CD.h_3}{2}=\frac{AB\left(h_1+h_2\right)}{2}=\frac{1}{2}S_{ABCD}\)
Vì AB = CD
Tương tự ta có \(S_{ADO}+S_{OBC}=\frac{AD\left(h_2+h_4\right)}{AB}=\frac{AD.BC}{2}=\frac{1}{2}S_{ABCD}\)
Vậy \(S_{OAB}+S_{ODC}=S_{ADO}+S_{OBC}\)
\(14+18=10+S_{OBC}\)
\(\Rightarrow....\)

diện tích hình tam giác obc là : (10 + 14 +18 ) : 2 +1 = 22 (cm2)
Đáp số : 22 cm2

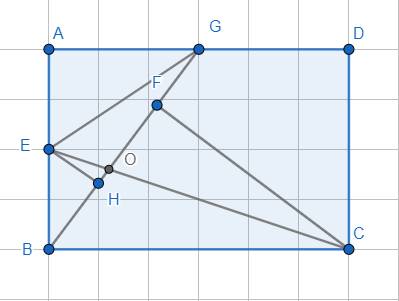
Kẻ \(EH\perp BG\), \(CF\perp BG\)
Ta có: \(S_{ABD}=S_{GBC}=\dfrac{1}{2}.AB.AD=\dfrac{1}{2}.S_{ABCD}\)
\(S_{BAG}=\dfrac{1}{2}.AB.AG=\dfrac{1}{2}.AB.\dfrac{1}{2}AD=\dfrac{1}{4}.AB.AD=\dfrac{1}{2}S_{ABD}\)
\(S_{GEB}=\dfrac{1}{2}.AG.EB=\dfrac{1}{2}.AG.\dfrac{1}{2}.AB=\dfrac{1}{4}.AG.AB=\dfrac{1}{2}S_{ABG}\)
\(\Rightarrow S_{GEB}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}S_{ABCD}=\dfrac{1}{8}S_{ABCD}=\dfrac{1}{4}S_{GBC}\)
\(\Leftrightarrow\dfrac{1}{2}.EH.BG=\dfrac{1}{4}.\dfrac{1}{2}CF.BG\)
\(\Leftrightarrow EH=\dfrac{1}{4}CF\)
Lại có: \(S_{OBE}=\dfrac{1}{2}OB.EH=\dfrac{1}{2}OB.\dfrac{1}{4}CF=\dfrac{1}{4}S_{OBC}\)
Ta có: \(S_{CBE}=S_{OBE}+S_{OBC}=S_{OBE}+4S_{OBE}=5S_{OBE}\)
\(S_{CBE}=5.10=50\left(cm^2\right)\)
Mà \(S_{CBE}=\dfrac{1}{2}S_{CBA}=\dfrac{1}{4}S_{ABCD}\Rightarrow S_{ABCD}=200\left(cm^2\right)\)
