Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trong tứ giác AOBM có 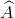 =
= 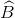 =
= 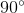 .
.
Suy ra cung AMB +  =
= 
=> cung AMB=  -
- 
=  -
- 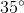
= 
b) Từ 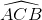 =
=  . Suy ra số đo cung nhỏ AB =
. Suy ra số đo cung nhỏ AB =  và số đo cung lớn AB :
và số đo cung lớn AB :
Cung AB = 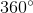 -
-  =
= 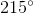

1. Để chứng minh cung DE có số đo không đổi, ta cần chứng minh góc \(\angle BOC\) có số đo không đổi. Thực vậy, theo tính chất hai tiếp tuyến cắt nhau, OB và OC là phân giác ngoài của tam giác ABC. Ta có
\(\angle BOC=180^{\circ}-\frac{\angle MBC}{2}-\frac{\angle NCB}{2}=\frac{\angle ABC}{2}+\frac{\angle ACB}{2}=90^{\circ}-\frac{\angle BAC}{2}=90^{\circ}-\frac{a}{2}\)
Do đó góc \(\angle BOC\) có số đo không đổi. Suy ra cung DE có số đo không đổi.
2. Do CD vuông góc với AB nên BC,BD là đường kính của hai đường tròn (O) và (O'). Suy ra
\(\angle CFB=\angle DEB=90^{\circ}\to\angle CFD=\angle CED=90^{\circ}.\) Vậy tứ giác CDEF nội tiếp. Do đó \(\angle ECF=\angle EDF\to\angle FAB=\angle ECF=\angle EDF=\angle EDB\)
Vậy AB là phân giác của góc AEF.
3. Đề bài có chút nhầm lẫn, "kẻ \(IH\perp BC\) mới đúng. Do tam giác ABC nhọn và I nằm trong nên các điểm H,K,L nằm trên các cạnh của tam giác. Sử dụng bất đẳng thức \(a^2+b^2\ge\frac{1}{2}\left(a+b\right)^2,\) ta suy ra \(AL^2+BL^2\ge\frac{1}{2}\left(AL+BL\right)^2=\frac{1}{2}AB^2.\) Tương tự ta cũng có \(BH^2+CH^2\ge\frac{1}{2}BC^2,KC^2+KA^2\ge\frac{1}{2}AC^2.\) Mặt khác theo định lý Pitago
\(AL^2+BH^2+CK^2=\left(IA^2-IL^2\right)+\left(IB^2-IH^2\right)+\left(IC^2-IK^2\right)\)
\(=\left(IA^2-IK^2\right)+\left(IB^2-IL^2\right)+\left(IC^2-IH^2\right)\)
\(=BL^2+CH^2+AK^2.\)
Thành thử \(AL^2+BH^2+CK^2=\frac{\left(AL^2+BL^2\right)+\left(BH^2+CH^2\right)+\left(CK^2+AK^2\right)}{2}\ge\frac{AB^2+BC^2+CA^2}{2}.\)
Dấu bằng xảy ra khi \(AL=BL,BH=CH,CK=AK\Leftrightarrow I\) là giao điểm ba đường trung trực.

VE HINH
â) Xét tứ giác KCID ,co:
gocI = (cungAB+cungCD):2 = (180+60):2 = 120 độ
gocK=(cungAB-cungCD):2 =(180-60):2=60 độ
gócI+gocK=120do+60do=180 do
Vay : tứ giác KCID nội tiếp (tổng số đo 2 góc đối diện=180 độ )
:góc AKB = 60 độ
b)Ta có:AB//CD
=>cungAC=cungBD=(180-60):2=60 do (2 cung nằm giữa 2 dây song song thì = nhau )
=>AC=BD(2 dây chan 2 cung = nhau thi = nhau ) (1)
=>tứ giác ACDB là hình thang cân
***Xét : 3giac AKDva 3giac BKC ,co:
gocD=gocC=90do (vi gocC va gocD là góc nội tiếp chắn nửa đường tròn)
gocCAD=gocDBC(2goc noi tiep cung chan cungCD)
AD=BC(2 đường chéo của hình thang cân thì = nhau )(cmt)
Do do:3giacAKD =3giacBKC (g-c-g)
=>KD=KC (2 canh tương ứng) (2)
Ta lại có :KA=KC+AC(C nam giua A va K)
}(3)
:KB=KD+BD(D nam giua B va K)
Tu (1) ,(2) va (3) suy ra KA=KB (4)
Tu (2) va (4) suy ra KA.KC=KB.KD .