Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

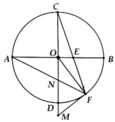
a, Học sinh tự chứng minh
b, Chứng minh: A F M ^ = C A F ^ ( = A C F ^ ) => MF//AC
c, Chứng minh: M F N ^ = M N F ^ => ∆MNF cân tại M => MN = MF
Mặt khác: OD = OF = R
Ta có MF là tiếp tuyến nên DOFM vuông => ĐPCM

Bài 2 nếu ai giải được thì làm ơn gửi cho mình cách giải nhé!!Mình cũng có bài này mà ko giải được

A B C D O M N K H E F I J T P
a) Ta có: Tứ giác ACBD nội tiếp (O;R) có 2 đường chéo là 2 đường kính vuông góc với nhau.
Nên tứ giác ACBD là hình vuông.
Xét tứ giác ACMH: ^ACM=^ACB=900; ^AHM=900
=> Tứ giác ACMH nội tiếp đường tròn
Do tứ giác ACBD là 1 hình vuông nên ^BCD=1/2.CAD=450
=> ^BCD=^MAN hay ^MCK=^MAK => Tứ giác ACMK nội tiếp đường tròn.
b) Gọi giao điểm của tia AE với tia tiếp tuyến BF là I. AF gặp MH tại J.
Ta có: Điểm E nằm trên (O) có đg kính AB => ^AEB=900
=> \(\Delta\)BEI vuông tại E. Dễ thấy \(\Delta\)BFE cân tại F => ^FEB=^FBE
Lại có: ^FEB+^FEI=900 => ^FBE+^FEI=900. Mà ^FBE+^FIE=900
Nên ^FEI=^FIE => \(\Delta\)EFI cân tại F => EF=IF. Mà EF=BF => BF=IF
Theo hệ quả của ĐL Thales ta có: \(\frac{MJ}{IF}=\frac{HJ}{BF}=\frac{AJ}{AF}\)=> MJ=HJ (Do IF=BF)
=> J là trung điểm của HM => Đpcm.
c) Trên tia đối của tia DB lấy T sao cho DT=CM.
Gọi P là hình chiếu của A xuống đoạn MN.
Dễ dàng c/m \(\Delta\)ACM=\(\Delta\)ADT (c.g.c) => ^CAM=^DAT và AM=AT
mà ^CAM phụ ^MAD => ^DAT+^MAD=900 => ^MAT=900
=> ^MAN=^TAN=1/2.^MAT=450.=> \(\Delta\)MAN=\(\Delta\)TAN (c.g.c)
=> ^AMN=^ATN (2 góc tương ứng) hay ^AMP=^ATD
=> \(\Delta\)APM=\(\Delta\)ADT (Cạnh huyền góc nhọn) => AD=AP (2 cạnh tương ứng).
Mà AD có độ dài không đổi (Vì AD=căn 2 . R) => AP không đổi.
Suy ra khoảng cách từ điểm A đến đoạn MN là không đổi
=> MN tiếp xúc với đường tròn tâm A cố định bán kính AD=căn 2.R.
Vậy...

 ღ༺Nhật༒Tân✰ ²ƙ⁶༻ღ
ღ༺Nhật༒Tân✰ ²ƙ⁶༻ღ
Sắp đến Tết rùi nè ae.Zui nhểy!Đứa nào đỗ nhớ khao tao nhá!
- Tên: ღ༺Nhật༒Tân✰ ²ƙ⁶༻ღ
- Đang học tại: Trường THCS Lập Thạch
- Địa chỉ: Huyện Lập Thạch - Vĩnh Phúc
- Điểm hỏi đáp: 16SP, 0GP
- Điểm hỏi đáp tuần này: 1SP, 0GP
- Thống kê hỏi đáp

d, Vi ED la tiep tuyen (chung minh tren) => tam giac EDF vuong tai D
co \(\widehat{CDE}=\frac{1}{2}sd\widebat{DC}=\frac{1}{2}\widehat{COD}=\frac{1}{2}.120=60^o\)
ma \(\widehat{CED}+\widehat{COD}=180^o\Rightarrow\widehat{CED}=180-120=60^o\)
suy ra \(\Delta CED\) deu => EC=CD (1)
mat khac cung co \(\widehat{CFD}=\widehat{CDF}\) (phu hai goc bang nhau)
=> tam giac CDF can tai C
suy ra CD=CF (2)
tu (1),(2) suy ra dpcm