
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) OBNC có NCO=OBN=90 nên OBNC là tứ giác nội tiếp
b) Xét tam giác ADC có AB,DC là các đường cao
mà AB cắt DC tại O
suy ra O là trực tâm của tam giác ADC
nên NO vuông góc với AD
c)
CONB là tứ giác nôi tiếp nên COA=CNB
Xét tam giác ACO và tam giác DCN
COA=CNB(cmt)
ACO=NCD=90
nên tam giác ACO đồng dạng với tam giác DNC
nên CA.CN=CO.CD
Còn câu d mk chịu

1: ΔOAM cân tại O
mà OC là trung tuyến
nên OC vuông góc AM
góc OBN+góc OCN=180 độ
=>OCNB nội tiếp
2: Xét ΔACO vuông tại C và ΔABN vuông tại B có
góc CAO chung
=>ΔACO đồng dạng với ΔABN
=>AC/AB=AO/AN
=>AC*AN=AO*AB

N thuộc tiếp tuyến Bx \(\Rightarrow\Delta ABN\) vuông tại B
M thuộc đường tròn \(\Rightarrow AM\perp BM\)
\(\Rightarrow BM\) là đường cao trong tam giác vuông ABN
Áp dụng hệ thức lượng: \(AB^2=AM.AN\)
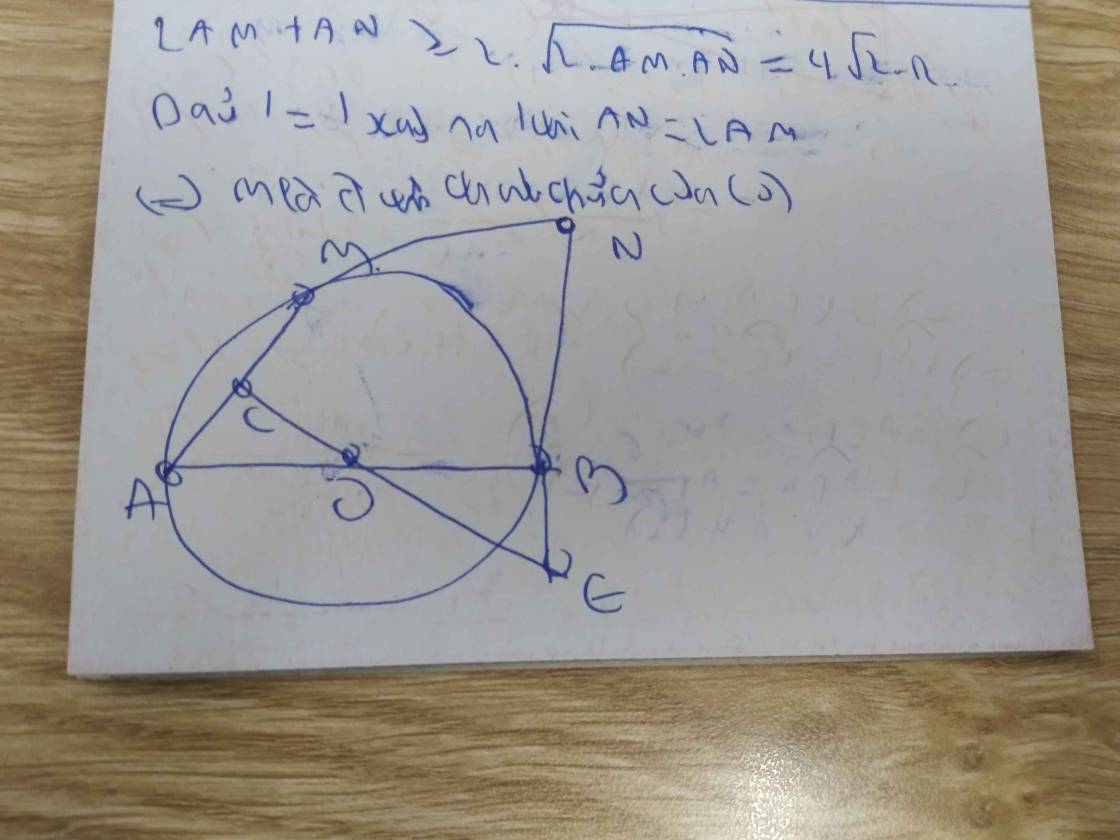
\(\Rightarrow2AM+AN\ge2\sqrt{2AM.AN}=2\sqrt{2AB^2}=2\sqrt{2}AB\)
Dấu "=" xảy ra khi và chỉ khi \(2AM=AN\Rightarrow M\) là trung điểm AN
\(\Rightarrow BM\) là trung tuyến ứng với cạnh huyền \(\Rightarrow BM=AM\)
\(\Rightarrow M\) là điểm chính giữa cung AB

a) Xét (O) có
ΔBMA nội tiếp đường tròn(B,M,A∈(O))
BA là đường kính(gt)
Do đó: ΔBMA vuông tại M(Định lí)
Xét (O) có
AB là đường kính của (O)(gt)
nên O là trung điểm của AB
Xét ΔBMA có
O là trung điểm của AB(gt)
C là trung điểm của AM(gt)
Do đó: OC là đường trung bình của ΔBMA(Định nghĩa đường trung bình của tam giác)
⇒OC//BM và \(OC=\dfrac{BM}{2}\)(Định lí 2 về đường trung bình của tam giác)
Ta có: OC//BM(cmt)
BM⊥BA(ΔBMA vuông tại M)
Do đó: OC⊥AM(Định lí 2 từ vuông góc tới song song)
Xét tứ giác OCNB có
\(\widehat{OCN}\) và \(\widehat{OBN}\) là hai góc đối
\(\widehat{OCN}+\widehat{OBN}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: OCNB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
b) Xét ΔNBA vuông tại B và ΔOCA vuông tại C có
\(\widehat{OAC}\) chung
Do đó: ΔNBA∼ΔOCA(g-g)
⇒\(\dfrac{AB}{AC}=\dfrac{AN}{AO}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AC\cdot AN=AO\cdot AB\)(đpcm)
c) Ta có: OC⊥AN(cmt)
mà E∈OC(gt)
nên EC⊥NA
Xét ΔNEA có
EC là đường cao ứng với cạnh NA(cmt)
AB là đường cao ứng với cạnh NE(gt)
EC cắt AB tại O(gt)
Do đó: O là trực tâm của ΔNEA(Định lí ba đường cao của tam giác)
⇒NO⊥AE(đpcm)

super easy!
theo hệ thức lượng và BĐT cô-si:
\(MF+2ME\ge2\sqrt{2MF.ME}=2\sqrt{2MN^2}=2MN\sqrt{2}\)
Vậy GTNN của MF+2ME là \(2MN\sqrt{2}\)
Đẳng thức xảy ra \(\Leftrightarrow\) \(\hept{\begin{cases}MF=2ME\\MF+2ME=2MN\sqrt{2}\end{cases}}\)
\(\Rightarrow\) \(2MF=2MN\sqrt{2}\)
\(\Leftrightarrow MF=MN\sqrt{2}\)
Ta có \(\sin F=\frac{MN}{MF}=\frac{1}{\sqrt{2}}\) nên \(\widehat{F}=45^0\)
Hay tam giác MNF vuông cân => ... => tam giác MNE vuông cân => ME = NE => E nằm chính giữa cung MN
p/s: làm bài tốt ko bn?