Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

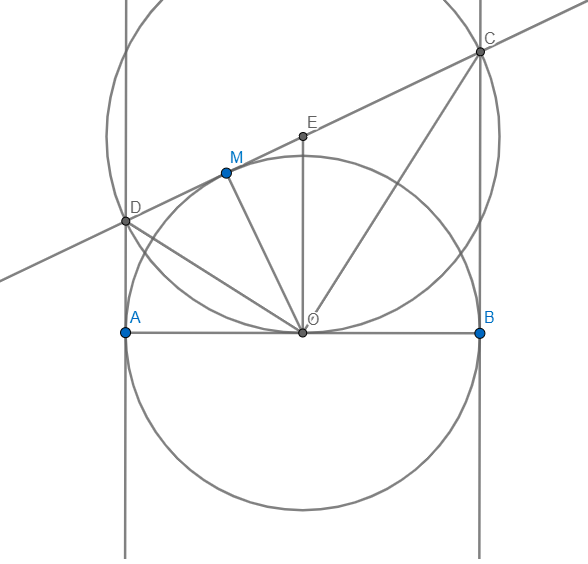
A B C D H E O
a/ Nối A với D ta có
\(\widehat{ADB}=90^o\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow AD\perp BC\)
=> H và D cùng nhìn AC dưới 1 góc vuông => AHDC là tứ giác nội tiếp
b/
Xét tg vuông ACO có
\(\widehat{ACO}+\widehat{AOC}=90^o\)
Ta có \(\widehat{ADH}+\widehat{EDB}=\widehat{ADB}=90^o\)
Xét tứ giác nội tiếp AHDC có
\(\widehat{ACO}=\widehat{ADH}\) (Góc nội tiếp cùng chắn cung AH)
\(\Rightarrow\widehat{AOC}=\widehat{EDB}\)
Xét tam giác EOH và tg EBD có
\(\widehat{BED}\) chung
\(\widehat{AOC}=\widehat{EDB}\)
=> tg EOH đồng dạng với tg EDB (g.g.g)
\(\Rightarrow\dfrac{EH}{EB}=\dfrac{EO}{ED}\Rightarrow EH.ED=EO.EB\)
a) Ta có \(\widehat{ADB}=90^0\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow\widehat{ADC}=90^0\)
Tứ giác \(AHDC\) có: \(\widehat{ADC}=\widehat{AHC}=90^0\) mà 2 góc này nội tiếp và chắn cung AC
\(\Rightarrow AHDC\) là tứ giác nội tiếp
b) Tứ giác \(AHDC\) nội tiếp \(\Rightarrow\widehat{ACO}=\widehat{ADE}\) (góc nội tiếp cùng chắn 1 cung)
Ta có: \(\widehat{EOH}=90^0-\widehat{ACO}=90^0-\widehat{ADE}=\widehat{EDB}\)
Xét \(\Delta EOH\) và \(\Delta EDB\) có:
\(\widehat{BED}\) chung
\(\widehat{EOH}=\widehat{EDB}\) (đã chứng minh)
\(\Rightarrow\Delta EOH\sim\Delta EDB\) (g.g) \(\Rightarrow\dfrac{EO}{EH}=\dfrac{ED}{EB}\Rightarrow EH.ED=EO.EB\)

a: Xét (O) có
DC,DA là tiếp tuyến
=>DC=DA và OD là phân giác của góc COA
=>OD vuông góc AC
Xét (O) có
EC,EB là tiếp tuyến
=>EB=EC và OE là phân giác của góc COB(2)
=>OE là trung trực của BC
=>OE vuông góc CB
AD+BE=DC+CE=DE
b: Từ (1), (2) suy ra góc DOE=1/2*180=90 độ
Xét tứ giác CMON có
góc CMO=góc CNO=góc MON=90 độ
=>CMON là hình chữ nhật
c: OM*OD+ON*OE
=OC^2+OC^2
=2*R^2ko đổi

b) Vì DA,DM là tiếp tuyến \(\Rightarrow OD\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOD=\dfrac{1}{2}\angle MOA\)
Vì CB,CM là tiếp tuyến \(\Rightarrow OC\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOC=\dfrac{1}{2}\angle MOB\)
\(\Rightarrow\angle MOC+\angle MOD=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)\)
\(\Rightarrow\angle COD=\dfrac{1}{2}\angle AOB=\dfrac{1}{2}.180=90\)
c) Vì \(\angle COD=90\Rightarrow O\in\) đường tròn đường kính CD
Gọi E là tâm đường tròn đường kính CD \(\Rightarrow E\) là trung điểm CD
Ta có: E là trung điểm CD,O là trung điểm AB và ABCD là hình thang
\(\Rightarrow EO\parallel AD\) \(\Rightarrow EO\bot AB\Rightarrow AB\) là tiếp tuyến của đường tròn đường kính CD

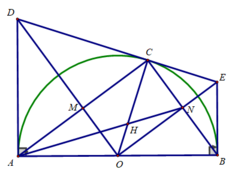
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật

\(\widehat{IAF}=\widehat{CAF}\)
\(\widehat{CFA}+\widehat{CAF}=90^0\)
\(\widehat{BAF}+\widehat{IAF}=90^0\)
\(\Rightarrow\widehat{CFA}=\widehat{BAF}\)
c.
O là trung điểm AB, G là trung điểm AI \(\Leftrightarrow\) OG là đường trung bình ABI
\(\Rightarrow OG//BI\Rightarrow OG\perp AC\)
Mà \(OA=OC\Rightarrow OG\) là trung trực AC
\(\Rightarrow AG=CG\Rightarrow CG\) là tiếp tuyến

O A B x C E D M
a, xét tg AEO và CEO có : EO chung
^AEO = ^CEO = 90
OA = OC = r
=> Tg AEO = tg CEO (ch-cgv)
=> ^AOE = ^COE
xét tg MAO và tg MCO có : Mo chung
OA = OC = r
=> tg MAO = tg MCO (cg-c)
=> ^MAO = ^MCO
mà ^MAO = 90
=> ^MCO = 90 => OC _|_ MC
có C thuộc 1/2(o)
=> MC là tt của 1/2(o)
b, xét tứ giác MCOA có : ^MCO = ^MAO = 90
=> ^MCO + ^MAO = 180
=>MCOA nội tiếp
+ có D thuộc 1/(o) dk AB (gt) => ^ADB = 90 = ADM
có MEA = 90 do AC _|_ MO (Gt)
=> ^ADM = ^MEA = 90
=> MDEA nt
Xét (O) có
ΔABC nội tiếp
AB là đường kính
=>ΔABC vuông tại C
=>BC vuông góc AC
Xét ΔKAB vuông tại A có AC là đường cao
nên BC*BK=BA^2=4*R^2