cho nửa (O) đường kính AB, trên bán kính OA, OB lần lượt lấy M, N sao cho OM=ON. từ M, N kẻ 2 tia song song cắt đường tr...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Trang Nguyễn

17 tháng 9 2021

cho nửa (O) đường kính AB, trên bán kính OA, OB lần lượt lấy M, N sao cho OM=ON. từ M, N kẻ 2 tia song song cắt đường tròn tại C, D. c/m: MC⊥CD

giúp mk vs ạ mk cần gấp

#Toán lớp 9

Từ công viễn

17 tháng 9 2021

Đúng(0)

Từ công viễn

17 tháng 9 2021

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Trang Nguyễn

16 tháng 9 2021

2) cho nửa (O) đường kính AB. trên bán kính OA, OB lần lượt lấy M, N sao cho OM=ON. từ M, N kẻ 2 tia song song cắt đường tròn tại C, D. c/m: MC ⊥CD

giúp mk vs ạ mk cần gấp

#Toán lớp 9

Trang Nguyễn

16 tháng 9 2021

2) cho nửa (O) đường kính AB. trên bán kính OA, OB lần lượt lấy M, N sao cho OM=ON. từ M, N kẻ 2 tia song song cắt đường tròn tại C, D. c/m: MC ⊥CD

giúp mk vs ạ mk cần gấp

#Toán lớp 9

Trang Nguyễn

16 tháng 9 2021

3) cho nửa (O) đường kính AB. trên bán kính OA, OB lần lượt lấy M, N sao cho OM=ON. từ M, N kẻ hai tia song song cắt đường tròn tại C và D. c/m: MC ⊥CD

giúp mk vs ạ mk đang cần gấp

#Toán lớp 9

Akai Haruma

Giáo viên

17 tháng 9 2021

Lời giải:
Kẻ đường kính $CT$ của $(O)$ thì $O$ là trung điểm $CT$

Xét tứ giác $CNTM$ có 2 đường chéo $CT,MN$ cắt nhau tại trung điểm $O$ của mỗi đường nên $CNTM$ là hình bình hành.

$\Rightarrow CM\parallel NT$. Mà CM\parallel DN$ nên $DN\parallel NT$ hay $D,N,T$ thẳng hàng.

Ta có: $\widehat{CDN}=\widehat{CDT}=90^0$ (góc nt chắn nửa đường tròn)

$\Rightarrow CD\perp DN$. Mà $DN\parallel MC$ nên $CD\perp MC$ (đpcm)

Đúng(0)

Akai Haruma

Giáo viên

17 tháng 9 2021

Hình vẽ:

Đúng(0)

Hoang nam khanh

23 tháng 9 2018 - olm

Cho nửa đường tròn tâm (o) đương kính AB .Trên bán kính OA,OB lần lượt lấy các điểmM và N sao cho OM bằng ỔN .Từ M và N vẽ hai tia song song cắt nửa đường tròn tại C và D .Chứng minh rằng :MC vuông góc với CD

#Toán lớp 9

Nhật Minh 7a2 54. Chu

13 tháng 10 2021

Cho đường tròn (O) đường kính AB. Trên các bán kính OA và OB lấy các điểm M và N sao cho OM = ON. Qua M và N lần lượt vẽ các dây CD và EF song song với nhau (C và E nằm cùng phía với AB). Từ O kẻ một đường thẳng vuông góc với 2 dây song song vừa vẽ, đường thẳng này cắt CD tại I và cắt FE tại J. Chứng minh: a) Tam giác OIM bằng tam giác OJN b) Hai dây CD và EF bằng nhau c) Tứ giác IJEC là hình chữ nhật d) Tứ giác CDFE là...

Đọc tiếp

#Toán lớp 9

Nguyễn Huỳnh Quốc Hy

28 tháng 7 2017 - olm

Cho đường tròn (O; R) đường kính AB. Trên các bán kính OA, OB lần lượt lấy các điểm M và N sao cho OM = ON. Qua M, N vẽ các dây cung CD, EF song song với nhau( C, E thuộc nửa đường tròn đường kính AB).

a) CMR: tứ giác CDFE là hình chữ nhật

b) Cho CM = 2/3 R, góc giữa CD và OA= 60 độ. Tính diện tích tứ giác CDFE

#Toán lớp 9

TRUONG LINH ANH

3 tháng 11 2017 - olm

cho đường tròn (O;R) đường kính AB từ điểm C trên tia đối của tia AB kẻ các tiếp tuyến CM,CN vs đường tròn (M,N là tiếp điểm )
a,CM CO vuông góc vs MN
b,tính MN bt OM=4cm,CO=6cm
c, vẽ đường kính MK tứ giác ABKN là hình j?vì sao?
d, một đường thẳng qua O song song vs MN cắt tia CM,CN lần lượt tại E và F.xác định vị trí của C trên tia đối của tia AB sao cho SABC là nhỏ nhất

#Toán lớp 9

Sách Giáo Khoa

27 tháng 4 2017

a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN

b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho AM = BN. Qua M và qua N kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD

#Toán lớp 9

Nguyen Thuy Hoa

23 tháng 6 2017

Đường kính và dây của đường tròn

Đúng(0)

Pham Trong Bach

12 tháng 6 2018

Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho AM = BN. Qua M và N kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD.

#Toán lớp 9

Cao Minh Tâm

12 tháng 6 2018

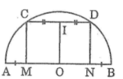
Giải sách bài tập Toán 9 | Giải bài tập Sách bài tập Toán 9

Ta có: MC // ND (gt)

Suy ra tứ giác MCDN là hình thang

Lại có: OM + AM = ON + BN (= R)

Mà AM = BN (gt)

Suy ra: OM = ON

Kẻ OI ⊥ CD (3)

Suy ra: IC = ID (đường kính dây cung)

Khi đó OI là đường trung bình của hình thang ACDN

Suy ra: OI // MC // ND (4)

Từ (3) và (4) suy ra: MC ⊥ CD, ND ⊥ CD.

Đúng(1)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP