Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

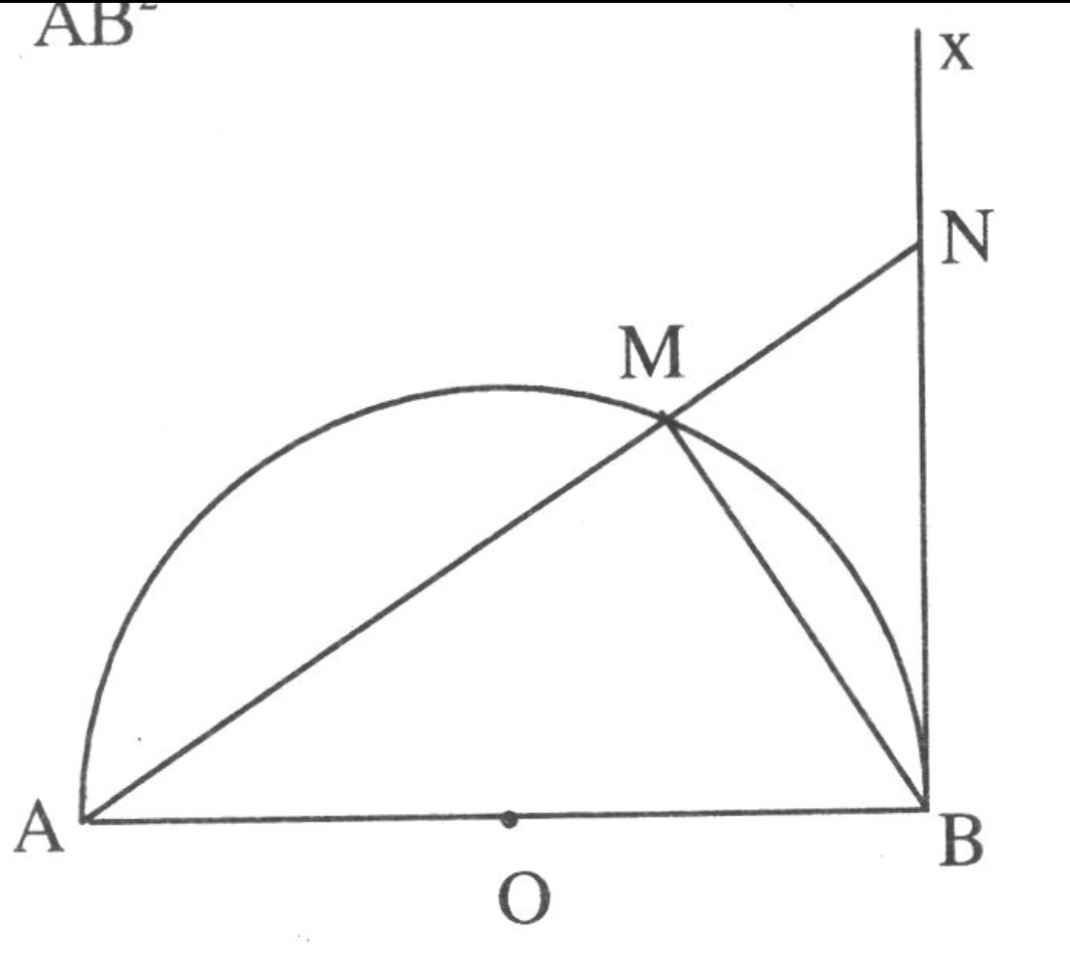
N thuộc tiếp tuyến Bx \(\Rightarrow\Delta ABN\) vuông tại B
M thuộc đường tròn \(\Rightarrow AM\perp BM\)
\(\Rightarrow BM\) là đường cao trong tam giác vuông ABN
Áp dụng hệ thức lượng: \(AB^2=AM.AN\)
\(\Rightarrow2AM+AN\ge2\sqrt{2AM.AN}=2\sqrt{2AB^2}=2\sqrt{2}AB\)
Dấu "=" xảy ra khi và chỉ khi \(2AM=AN\Rightarrow M\) là trung điểm AN
\(\Rightarrow BM\) là trung tuyến ứng với cạnh huyền \(\Rightarrow BM=AM\)
\(\Rightarrow M\) là điểm chính giữa cung AB

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')