Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì BE vuông góc với AC tại E (E ϵAC) ⇒ góc BEC =\(90^0\)
Vì CF vuông góc với AB tại F (F ϵ AB) ⇒ góc BFC =\(90^0\)
xét tứ giác BCEF có ;
góc BEC+BFC=\(90^0+90^0=180^0\)
mà hai góc ở vị trí kề nhau
⇒tứ giác BCEF là tgnt hay A,C,E,F cùng nằm trên một đtròn
b,

a. Em tự giải
b.
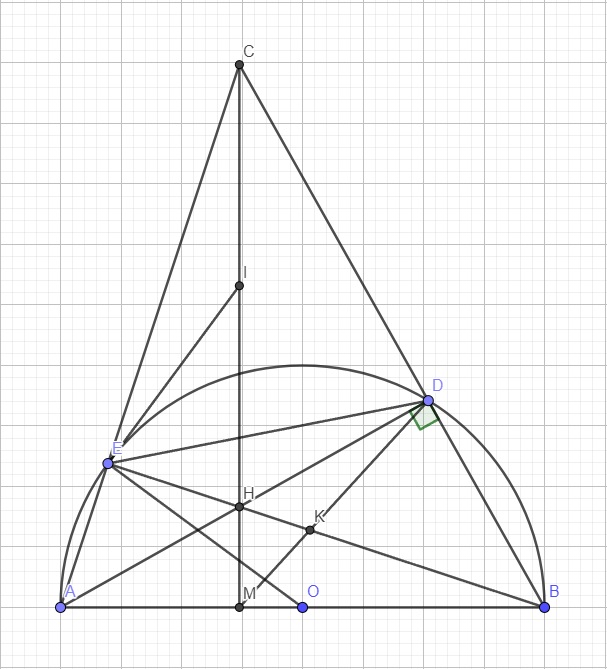
Do tứ giác BDHM nội tiếp \(\Rightarrow\widehat{HDM}=\widehat{HBM}\) (cùng chắn cung HM)
Do tứ giác ABDE nội tiếp \(\Rightarrow\widehat{HBM}=\widehat{ADE}\) (cùng chắn cung AE)
\(\Rightarrow\widehat{HDM}=\widehat{ADE}\)
\(\Rightarrow DH\) là phân giác trong góc \(\widehat{EDK}\) của tam giác EDK
Lại có \(DH\perp DB\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow DB\) là phân giác ngoài góc \(\widehat{EDK}\) của tam giác EDK
Áp dụng định lý phân giác:
\(\dfrac{EH}{HK}=\dfrac{EB}{BK}=\dfrac{ED}{DK}\) \(\Rightarrow BK.HE=BE.HK\)
c.
Hai điểm D và E cùng nhìn CH dưới 1 góc vuông nên tứ giác CDHE nội tiếp đường tròn đường kính CH
\(\Rightarrow I\) là trung điểm CH
Trong tam giác ABC, do hai đường cao AD và BE cắt nhau tại H \(\Rightarrow H\) là trực tâm
\(\Rightarrow CH\perp AB\) hay C;H;M thẳng hàng
Ta có \(IC=IE\) (do I là tâm đường tròn ngoại tiếp CDE) \(\Rightarrow\Delta CIE\) cân tại I
\(\Rightarrow\widehat{ECI}=\widehat{CEI}\)
Lại có \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O \(\Rightarrow\widehat{OBE}=\widehat{OEB}\)
Mà \(\widehat{OBE}=\widehat{ECI}\) (cùng phụ \(\widehat{BAC}\))
\(\Rightarrow\widehat{CEI}=\widehat{OEB}\)
\(\Rightarrow\widehat{CEI}+\widehat{IEB}=\widehat{OEB}+\widehat{IEB}\)
\(\Rightarrow\widehat{CEB}=\widehat{OEI}\)
\(\Rightarrow\widehat{OEI}=90^{ }\)
Hay \(OE\perp IE\Rightarrow IE\) là tiếp tuyến của đường tròn tâm O

O A B C H D I J E
a) Ta có: ^CBH=^ACH (Cùng phụ ^HCB) (1)
Xét \(\Delta\)CHD: I và J lần lượt là trung điểm của CH & DH => IJ là đường trung bình \(\Delta\)CHD
=> IJ // CD => IJ // AC => ^CIJ=^ACH (So le trg) (2)
Từ (1) và (2) => ^CIJ=^CBH (đpcm).
b) Thấy CJ là đường trung bình của tam giác ADH => \(\frac{CJ}{AH}=\frac{1}{2}\)
Mà \(\frac{HI}{CH}=\frac{1}{2}\)(Do I là trg điểm CH) => \(\frac{CJ}{AH}=\frac{HI}{CH}\Rightarrow\frac{CJ}{HI}=\frac{AH}{CH}\)
Dễ c/m \(\Delta\)AHC ~ \(\Delta\)CHB => \(\frac{AH}{CH}=\frac{CH}{HB}\Rightarrow\frac{CJ}{HI}=\frac{CH}{HB}\)
Lại có: CJ//AB và CH vuông AB => CH vuông CJ => ^JCH=900
Xét \(\Delta\)CJH và \(\Delta\)HIB: ^JCH=^IHB; \(\frac{CJ}{CH}=\frac{CH}{HB}\)=> \(\Delta\)CJH~\(\Delta\)HIB (c.g.c) (đpcm).
c) Ta có: ^HIB + ^HBI = 900. Mà ^HBI=^CHJ (Do \(\Delta\)CJH~\(\Delta\)HIB) => ^HIB+^CHJ=900
=> Tam giác HEI vuông tại E => ^IEJ=900
Xét tứ giác CIEJ: ^IEJ=^ICJ=900 => Tứ giác CIEJ nội tiếp đường tròn
=> ^ECI=^EJI hay ^ECH=^HJI. Mà ^HJI=^HDC (Vì IJ//CD) => ^ECH=^HDC
Xét \(\Delta\)HEC và \(\Delta\)HCD: ^ECH=^CDH (cmt); ^CHD chung => \(\Delta\)HEC~\(\Delta\)HCD (g.g)
Suy ra: \(\frac{HE}{HC}=\frac{HC}{HD}\Rightarrow HE.HD=HC^2\)(đpcm).
có vài chỗ bạn ghi nhầm nha, may là mình cũng thuộc hàng top của huyện nên mới hiểu đc đó

a) Tự làm nhá
b) +) CM \(\Delta ADC~\Delta HDE\left(g-g\right)\)
=> DA.HE=DH.AC
+) \(\Delta BAD\)cân\(=>\widehat{BAD}=90^0-\frac{1}{2}\widehat{B}=\widehat{CAD}\)
mà \(\widehat{CAD}=\widehat{B}\)
=> AD là tia phân giác góc HAC => Góc HAE = góc CAE => cung HE= cung CE => cạnh HE = cạnh CE => tam giác cân (dpcm)
3) Xét \(\Delta MNP\)zuông tại M ngoại tiếp đươg tròn tâm I , bán kính r , tiếp xúc các cạnhMN , MP,NP thứ tự tại D, E ,F
ta có \(\widehat{IEM}=\widehat{IDM}=\widehat{DME}=90\);ID =IE=r
=> tứ giác IEMD là hình zuông
=> MD=ME=r
Có ND=NF,PE =PF( các tia tiếp tuyến cắt nhau)
=> MN+MP-NP=MD+ND+ME+PE-NF-PF=MD+ME=2r
tam giác ABH zuông tại H có \(\hept{\begin{cases}R_1=\frac{AH+BH-AB}{2}\\\end{cases}}\)
Tam giác ACH zuông tại H có \(R_2=\frac{AH+CH-AC}{2}\)
tam giác ABC zuông tại A có \(R_3=\frac{AB+AC-BC}{2}\)
\(=>R_1+R_2+R_3=AH\)
ta có \(AH\le AO=\frac{6}{2}=3cm\)
dấu = xảy ra khi H trung O
=> A là điểm chính giữa cung BC
Nguồn : https://qanda.ai/vi/solutions/npWTTopujG-Cho-n%E1%BB%ADa-%C4%91%C6%B0ong-tr%C3%B2n-t%C3%A2m-O-d%C6%B0%E1%BB%9Dng-k%C3%ADnh-BC6cm-Tr%C3%AAn-n%E1%BB%ADa-%C4%91%C6%B0%E1%BB%9Dng-tr%C3%B2n