Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
CA,CE là các tiếp tuyến
Do đó: CA=CE và OC là phân giác của góc AOE
Xét (O) có
DE,DB là các tiếp tuyến
Do đó: DE=DB và OD là phân giác của góc EOB
Ta có: CA+DB
=CE+DE
=CD
b: Ta có: OC là phân giác của góc AOE
=>\(\widehat{AOE}=2\cdot\widehat{EOC}\)
OD là phân giác của góc EOB
=>\(\widehat{EOB}=2\cdot\widehat{EOD}\)
Ta có: \(\widehat{AOE}+\widehat{BOE}=180^0\)(hai góc kề bù)
=>\(2\cdot\widehat{EOC}+2\cdot\widehat{EOD}=180^0\)
=>\(2\cdot\left(\widehat{EOC}+\widehat{EOD}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)

1: Xét (O) có
CA,CM là tiếp tuyến
=>CA=CM và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là tiếp tuyến
=>DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COM+góc DOM=1/2(góc MOA+góc MOB)
=>góc COD=1/2*góc AOB=90 độ
2: CD=CM+MD
mà CM=CA và MD=DB
nên CD=CA+DB
3: AC*BD=CM*MD
Xét ΔOCD vuông tại O có OM là đường cao
nên CM*MD=OM^2
=>AC*BD=R^2 không đổi

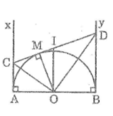
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
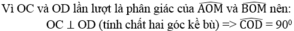
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.

Câu này hơi kì, vì đề đã nói rõ tiếp tuyến cắt Oz tại M, thế thì M chạy trên tia Oz còn hỏi gì nữa???
mình nghĩ câu này, nên "giấu" cái Oz đi, mà cho M là trung điểm của CD, làm thế nhé
Thấy tứ giác ABDC là hình thang vuông, có OM là đường trung bình (qua trung điểm 2 cạnh bên)
=> OM // Ax // By => M chạy trên tia qua O và // Ax (chính là Oz)

A B x y C D M O
a/
Xét tg vuông OAC và tg vuông OMC có
OA=OM=R
OC chung
=> tg OAC = tg OMC (Hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{AOC}=\widehat{MOC}=\dfrac{\widehat{AOM}}{2}\)
Tương tự ta cũng có
tg OBD = tg OMD \(\Rightarrow\widehat{BOD}=\widehat{MOD}=\dfrac{\widehat{BOM}}{2}\)
\(\Rightarrow\widehat{MOC}+\widehat{MOD}=\widehat{COD}=\dfrac{\widehat{AOM}}{2}+\dfrac{\widehat{BOM}}{2}=\dfrac{180^o}{2}=90^o\)
b/
AB+BD nhỏ nhất khi \(M\equiv B\)

b: Xét (O) có
CM là tiếp tuyến
CA là tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM là tiếp tuyến
DB là tiếp tuyến
Do đó: DM=DB
Ta có: CM+MD=CD
nên CD=AC+BD