Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì AH, HB, AB đều là các đường kính của các nửa đường tròn (O1) , (O2) và (O) nên tứ giác MPHQ có ba góc P, Q, M vuông. Vì vậy nó là hình chữ nhật.
Từ đó, ta có HM = PQ.
b) Vì MHPQ là hình chữ nhật nên \widehat{MPQ}=\widehat{MHQ}=\widehat{MBH}\left(=\dfrac{\stackrel\frown{HQ}}{2}\right)MPQ=MHQ=MBH(=2HQ⌢), do đó APQB là tứ giác nội tiếp.
c) Ta có \widehat{O_1PA}=\widehat{PAO_1}=90^o-\widehat{HMP}=90^o-\widehat{MPQ}O1PA=PAO1=90o−HMP=90o−MPQ
\Rightarrow\widehat{O_1PA}+\widehat{MPQ}=90^o\Rightarrow\widehat{O_1PQ}=90^o⇒O1PA+MPQ=90

Câu hỏi của Mafia - Toán lớp 9 - Học toán với OnlineMath
Em có thể tham khảo tại đây nhé.

OMABICDEF
a) Ta thấy OAM và OBM là các tam giác vuông có chung cạnh huyền OM nên A, O, B, M cùng thuộc đường tròn đường kính OM.
b) Theo tính chất hai tiếp tuyến cắt nhau thì MA = MB và MI là tia phân giác góc AMB.
Vậy thì tam giác MAB cân tại M, có phân giác MI đồng thời là đường cao.
Vậy nên \(OM\perp AB\) tại I.
c) Do D thuộc đường tròn (O) nên OC = OB = OD.
Suy ra tam giác BDC vuông tại D.
Xét tam giác vuông CBM, đường cao BD, ta có: \(MD.MC=BM^2\) (Hệ thức lượng)
Xét tam giác vuông OBM, đường cao BI, ta có: \(MI.MO=BM^2\) (Hệ thức lượng)
Vậy nên MD.MC = MI.MO
d) Ta thấy CEF và CAF là các tam giác vuông có chung cạnh huyền CF nên FAEC nội tiếp đường tròn đường kính CF.
\(\Rightarrow\widehat{FCE}=\widehat{EAB}\) (Hai góc nội tiếp cùng chắn cung CO)
Lại có O,E, A, M, B cùng thuộc đường tròn đường kính OM nên \(\widehat{EAB}=\widehat{EMB}\) (Hai góc nội tiếp cùng chắn cung EB)
\(\Rightarrow\widehat{FCE}=\widehat{EMB}\)
Ta có \(\widehat{EMB}+\widehat{ECB}=90^o\Rightarrow\widehat{FCE}+\widehat{ECB}=90^o\)
\(\Rightarrow\widehat{FCB}=90^o\)
Vậy FC là tiếp tuyến của đường tròn (O).

a) Ta thấy CA, CE là hai tiếp tuyến của đường tròn tâm O nên theo tính chất hai tiếp tuyến cắt nhau ta có:
\(\widehat{COA}=\widehat{COE}\)
Tương tự \(\widehat{DOE}=\widehat{DOB}\)
Suy ra \(\widehat{DOE}+\widehat{COE}=\widehat{DOB}+\widehat{COA}\Rightarrow\widehat{COD}=\widehat{DOB}+\widehat{COA}\)
Mà \(\widehat{DOB}+\widehat{COA}+\widehat{COD}=180^o\Rightarrow\widehat{COD}=90^o\)
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có \(OC\perp AE\)
\(\Rightarrow\widehat{OAE}=\widehat{ACO}\) (Cùng phụ với góc AOC)
Mà \(\widehat{ACO}=\widehat{ECO}\Rightarrow\widehat{COD}=\widehat{EAB}\)
Vậy thì \(\Delta AEB\sim\Delta COD\left(g-g\right)\)
c) Gọi I là trung điểm CD. Xét hình thang ACDB có IO là đường trung bình nên IO // AC//BD
Vậy nên OI vuông góc với AB tại O, hay AB là tiếp tuyến tại O của đường tròn (I, CD/2)

a) Do C thuộc nửa đường tròn nên \(\widehat{ACB}=90^o\) hay AC vuông góc MB.
Xét tam giác vuông AMB có đường cao AC nên áp dụng hệ thức lượng ta có:
\(BC.BM=AB^2=4R^2\)
b) Xét tam giác MAC vuông tại C có CI là trung tuyến ứng với cạnh huyền nên IM = IC = IA
Vậy thì \(\Delta ICO=\Delta IAO\left(c-c-c\right)\)
\(\Rightarrow\widehat{ICO}=\widehat{IAO}=90^o\)
Hay IC là tiếp tuyến tại C của nửa đường tròn.
c) Xét tam giác vuông AMB có đường cao AC, áp dụng hệ thức lượng ta có:
\(MB.MC=MA^2=4IC^2\Rightarrow IC^2=\frac{1}{4}MB.MC\)
Xét tam giác AMB có I là trung điểm AM, O là trung điểm AB nên IO là đường trung bình tam giác ABM.
Vậy thì \(MB=2OI\Rightarrow MB^2=4OI^2\) (1)
Xét tam giác vuông MAB, theo Pi-ta-go ta có:
\(MB^2=MA^2+AB^2=MA^2+4R^2\) (2)
Từ (1) và (2) suy ra \(4OI^2=MA^2+4R^2.\)
d) Do IA, IC là các tiếp tuyến cắt nhau nên ta có ngay \(AC\perp IO\Rightarrow\widehat{CDO}=90^o\)
Tương tự \(\widehat{CEO}=90^o\)
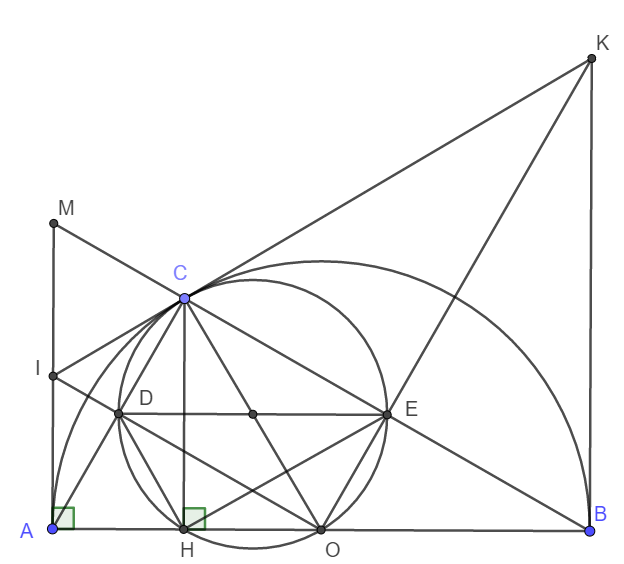
Xét tứ giác CDOE có \(\widehat{CEO}=\widehat{CDO}=90^o\)mà đỉnh E và D đối nhau nên tứ giác CDOE nội tiếp đường tròn đường kính CO.
Xét tứ giác CDHO có: \(\widehat{CHO}=\widehat{CDO}=90^o\) mà đỉnh H và D kề nhau nên CDHO nội tiếp đường tròn đường kính CO.
Vậy nên C, D, H , O, E cùng thuộc đường tròn đường kính CO.
Nói cách khác, O luôn thuộc đường tròn ngoại tiếp tam giác HDE.
Vậy đường tròn ngoại tiếp tam giác HDE luôn đi qua điểm O cố định.

A B O C H D E F
a) Do C thuộc đường tròn nên \(\widehat{ACB}=90^o\)
Áp dụng định lý Pi-ta-go: \(BC=\sqrt{10^2-6^2}=8\left(cm\right)\)
Xét tam giác vuông ACB, đường cao CH. Áp dụng hệ thức lượng trong tam giác, ta có:
\(CH.AB=CA.BC\Rightarrow CH=\frac{6.8}{10}=4,8\left(cm\right)\)
Ta thấy \(sin\widehat{ABC}=\frac{AC}{AB}=\frac{6}{10}\Rightarrow\widehat{ABC}\approx36^o52'\)
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có: \(DC=DB\) và DO là phân giác góc BDC.
Vậy thì DO cũng là đường trung trực của BC hay \(DO\perp BC.\)
c) Xét tam giác vuông ABC, đường cao CH, ta có : \(AH.AB=AC^2\) (Hệ thức lượng)
Xét tam giác vuông AEB, đường cao AC, ta có: \(AC^2=EC.CB\) (Hệ thức lượng)
Vậy nên \(AH.AB=EC.CB\)
d) Ta thấy HC // AE (Cùng vuông góc với AB)
Áp dụng Ta let ta có: \(\frac{IH}{AF}=\frac{IC}{EF}\left(=\frac{IB}{FB}\right)\)
mà IH = IC nên AF = FE.
Xét tam giác vuông ACE có F là trung điểm cạnh huyền nên FA = FE = FC.
Xét tam giác FAO và FCO có: FO chung, FA = FC, AO = CO nên \(\Delta FAO=\Delta FCO\left(c-c-c\right)\)
\(\Rightarrow\widehat{FCO}=\widehat{FAO}=90^o\)
Vậy nen FO là tiếp tuyến của đường tròn.

Đường tròn c: Đường tròn qua B_1 với tâm O Đoạn thẳng j: Đoạn thẳng [A, B] Đoạn thẳng k: Đoạn thẳng [O, M] Đoạn thẳng l: Đoạn thẳng [M, H] Đoạn thẳng m: Đoạn thẳng [H, O] Đoạn thẳng n: Đoạn thẳng [A, M] Đoạn thẳng p: Đoạn thẳng [M, B] Đoạn thẳng q: Đoạn thẳng [A, O] Đoạn thẳng r: Đoạn thẳng [O, B] Đoạn thẳng t: Đoạn thẳng [N, B] Đoạn thẳng b: Đoạn thẳng [E, J_1] Đoạn thẳng e: Đoạn thẳng [N, E] Đoạn thẳng f_1: Đoạn thẳng [E, B] Đoạn thẳng g_1: Đoạn thẳng [A, E] O = (6.36, -0.08) O = (6.36, -0.08) O = (6.36, -0.08) Điểm M: Điểm trên f Điểm M: Điểm trên f Điểm M: Điểm trên f Điểm H: Giao điểm đường của f, g Điểm H: Giao điểm đường của f, g Điểm H: Giao điểm đường của f, g Điểm A: Giao điểm đường của c, h Điểm A: Giao điểm đường của c, h Điểm A: Giao điểm đường của c, h Điểm B: Giao điểm đường của c, i Điểm B: Giao điểm đường của c, i Điểm B: Giao điểm đường của c, i Điểm I: Giao điểm đường của g, j Điểm I: Giao điểm đường của g, j Điểm I: Giao điểm đường của g, j Điểm K: Giao điểm đường của j, k Điểm K: Giao điểm đường của j, k Điểm K: Giao điểm đường của j, k Điểm N: A đối xứng qua F Điểm N: A đối xứng qua F Điểm N: A đối xứng qua F Điểm E: Giao điểm đường của a, k Điểm E: Giao điểm đường của a, k Điểm E: Giao điểm đường của a, k Điểm J: Trung điểm của A, N Điểm J: Trung điểm của A, N Điểm J: Trung điểm của A, N
a) Theo tính chất hai tiếp tuyến cắt nhau, ta có tam giác MAB cân tại M có MK là phân giác nên đồng thời là đường trung tuyến. Vậy thì K là trung điểm AB hay \(AK=\frac{AB}{2}\)
Ta thấy các tam giác MHO, MAO, MBO đều là các tam giác vuông chung cạnh huyền MO nên M, H, A, O B cùng thuộc đường tròn đường kính MO.
b) Do K là trung điểm AB nên theo tính chất đường kính dây cung, ta có \(\widehat{IKO}=90^o\)
Suy ra \(\Delta IKO\sim\Delta MHO\left(g-g\right)\Rightarrow\frac{OI}{OM}=\frac{OK}{OH}\Rightarrow OI.OH=OM.OK\)
Xét tam giác vuông MBO, đường cao BK, ta có: \(OK.OM=OB^2=R^2\)
Vậy nên \(OI.OH=OK.OM=R^2\)
c) Ta thấy do trung điểm của BN cắt OM tại E nên EN = EB
Lại có EB = EA vì OM là đường trung trực của AB
Suy ra EA = EN hay tam giác EAN cân tại E.
Gọi J là trung điểm AN.
Xét tam giác cân EAN có EJ là trung tuyến nên đồng thời là đường cao.
Vậy thì \(EJ\perp OA\) hay EJ // AM.
Xét tam giác OAM, áp dụng định lý Talet ta có:
\(\frac{OE}{OM}=\frac{OF}{OA}=\frac{2}{3}\)

a) AB và AC là tiếp tuyến của (O;R) =>AB⊥OB và AC⊥OC =>B và C nhìn OA góc 90° =>B và C cùng nằm trên đường tròn đường kính AO hay A,B,C,) cùng nằm trên đường tròn đường kính AO.
Hai △AOB và △AOC là 2 tam giác vuông có chung cạnh huyền OA và 2 cạnh góc vuông OB=OC (cùng = R) => △AOB = △AOC =>OA là phân giác ∠BOC mà △BOC cân tại B =>OA là đường trung trực của BC.
b)xét △ODB và △OBA có 2 góc vuông tại D và B, chung góc nhọn tại O =>△ODB ∼ △OBA =>OD/OB=OB/OA =>OA.OD=OB²=R².

O A C B D H I M
a) Tam giác COD và HOD là các tam giác vuông có chung cạnh huyền OD nên O, H, D, C cùng thuộc đường tròn đường kính OD.
b) Theo tính chất hai tiếp tuyến cắt nhau, ta có \(OD\perp BC\)
Tam giác DIA và DHA là hai tam giác vuông có chung cạnh AD nên DIHA là tứ giác nội tiếp.
Vậy thì \(\widehat{IDA}=\widehat{IHO}\)
Từ đó ta có \(\Delta IOH\sim\Delta AOD\left(g-g\right)\Rightarrow\frac{OI}{OA}=\frac{OH}{OD}\Rightarrow OH.OA=OI.OD\)
c) Xét tam giác vuông DBO, chiều cao BI, ta có:
\(OI.OD=OB^2\) (Hệ thức lượng)
Mà \(OB^2=OM^2;OI.OD=OH.OA\Rightarrow OM^2=OH.OA\)
\(\Rightarrow\Delta OHM\sim\Delta OMA\left(c-g-c\right)\Rightarrow\widehat{OMA}=\widehat{OHM}=90^o\)
Vậy AM là tiếp tuyến của đường tròn (O).

có góc AQB= 90 độ( góc nội tiếp chắn nửa đường tròn tâm O) Hay góc AQP=90 độ => góc QAP= 90 độ- góc QPA=90 độ-1/2sđ cung AP
có góc APC= 90 độ( góc nội tiếp chắn nửa đường tròn tâm O1)=> góc PAC=90 độ - góc PCA=90 độ - 1/2sđ cung AP
Vì vậy góc QAP= góc PAC hay AP là tia phân giác của góc QAB
Ta có: góc BQA =90o (góc nội tiếp chắn nửa (O))
Xét Δ PQA vuông tại Q có: góc QAP + góc QPA =90o ⇒ góc QAP=90o- góc QPA
Mà góc QPA =1/2 sđ cung PA ( góc QPA là góc tạo bởi tia tiếp tuyến cà dây cung chắn cung AP của (O1))
⇒góc QAP=90o- 1/2 sđ cung PA (1)
Xét ΔCPA vuông tại P ( vì góc CPA là góc nội tiếp chắn nửa (O1)) có
góc PCA + góc PAC =90o⇒góc PAC =90o-góc PCA
mà góc PCA =1/2 sđ cung PA ( góc nội tiếp chắn cung PA )
⇒góc PAC= 90o-1/2 sđ cung PA (2)
Từ (1) và (2) ⇒ góc QAP=góc PAC ⇒ AP là tia phân giác của góc QAB