Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

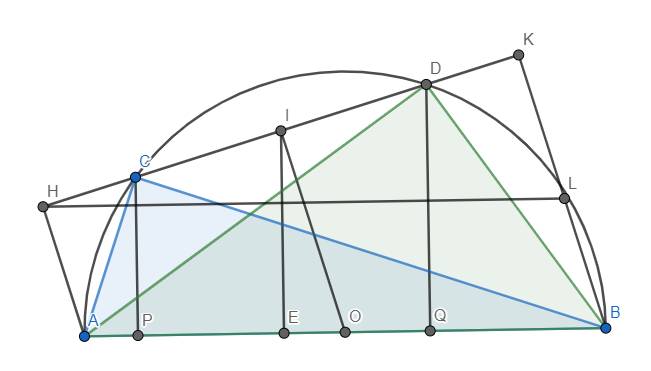
a) Ta thấy OI//AH//BK \(\left(\perp CD\right)\).
Xét hình thang ABKH (AH//BK), O là trung điểm AB. OI//AH \(\left(I\in HK\right)\) nên I là trung điểm HK.
b) Hạ \(CP\perp AB\) tại P, \(DQ\perp AB\) tại Q. Khi đó IE//CP//DQ \(\left(\perp AB\right)\).
Xét hình thang CDQP (CP//DQ) có I là trung điểm CD (hiển nhiên), IE//CP và \(E\in PQ\) nên IE là đường trung bình của hình thang CDQP \(\Rightarrow IE=\dfrac{CP+DQ}{2}\)
Lại có \(S_{ACB}=\dfrac{1}{2}AB.CP\), \(S_{ADB}=\dfrac{1}{2}.AB.DQ\)
\(\Rightarrow S_{ACB}+S_{ADB}=AB.\dfrac{CP+DQ}{2}=AB.IE\) (đpcm)
c) Ta có \(S_{AHKB}=\dfrac{AH+BK}{2}.HK=OI.HK\)
Do dây CD có độ dài không đổi nên khoảng cách từ O đến dây CD là OI cũng không đổi. Như vậy ta chỉ cần tìm vị trí của C để HK lớn nhất.
Thật vậy, dựng hình bình hành ABLH. Khi đó vì BK//AH nên \(L\in BK\). Đồng thời ta luôn có \(HK\le HL=AB\), suy ra \(S_{AHKB}\le OI.AB\).
Dấu "=" xảy ra \(\Leftrightarrow HK=HL\) \(\Leftrightarrow K\equiv L\) \(\Leftrightarrow\) AHKB là hình bình hành \(\Leftrightarrow\) HK//AB hay CD//AB \(\Rightarrow OI\perp AB\). Vậy C là điểm sao cho \(OI\perp AB\).
(Nếu muốn tìm cụ thể vị trí của C, thì mình nói luôn nó là điểm C sao cho \(sđ\stackrel\frown{AC}=180^o-2arc\cos\left(\dfrac{CD}{AB}\right)\) nhé. Chứng minh cái này dễ, mình nhường lại cho bạn.)
Chỗ vị trí C mình sửa lại là \(sđ\stackrel\frown{AC}=90^o-arc\sin\dfrac{CD}{AB}\) nhé.

a) gọi I là trung điểm của CD ta có IC=ID (1)
mặt khác OI _|_ CD nên OI//AH//BK => IH=IK(2)
từ (1) và (2) => CH=DK (đpcm)
b) Gọi C', I', D' lần lượt là hình chiếu của C,I,D trên AB
\(\Delta HIE=\Delta KIF\left(ch.gn\right)\Rightarrow S_{AHKB}=S_{AEFB}=AB\cdot II'\)
ta lại có \(S_{ACB}=\frac{1}{2}AB\cdot CC'\left(3\right);S_{ADB}=\frac{1}{2}AB\cdot DD'\left(4\right)\)
mặt khác \(\frac{CC'+DD'}{2}=II'\left(5\right)\)
từ (3), (4) và (5) ta có \(S_{ACB}+S_{ABD}=AB\cdot II'=S_{AHKB}\)(chỗ này theo mình là SAHKB)
c) \(OI=\sqrt{\frac{AB^2}{4}-\frac{CD^2}{4}}=12\left(cm\right)\)
\(S_{AHKB}=S_{AEFB}=AB\cdot II'\le AB\cdot OI\)
dấu "=" xảy ra khi \(II'=OI\)hay \(OI\perp AB\)lúc này CD //AB
vậy GTLN của \(S_{AHKB}=AB\cdot OI=12\cdot30=360\left(cm^2\right)\)

B O A C D K H E
a, Xét tứ giác AKCH có: \(\widehat{AKC}+\widehat{AHC}=90+90=180\)=> tứ gác AKCH nội tiếp
b,Tứ giác AKCH nội tiếp => \(\widehat{HCK}=\widehat{HAD}\)(góc trong và góc ngoài đỉnh đối diện)
Mặt khác: \(\widehat{HAD}=\widehat{BCD}=\frac{1}{2}sđ\widebat{BD}\)
=> \(\widehat{BCD}=\widehat{ACD}\)=> CD là phân giác \(\widehat{KCB}\)
c, Tứ giác AKCH nội tiếp: => \(\widehat{CKE}=\widehat{CAH}\)
Mà: \(\widehat{CDB}=\widehat{CAH}=\frac{1}{2}sđ\widebat{BC}\)
=> \(\widehat{CKE}=\widehat{CDE}\)=> tứ giác CKDE nội tiếp
=> \(\widehat{CKD}+\widehat{CED}=180\Rightarrow\widehat{CED}=180-\widehat{CKD}=180-90=90\)
=> \(CE⊥BD\)(ĐPCM)
d, em xem lại xem có gõ sai đề không nhé
Câu d) Khi C di chuyển trên cung nhỏ̉ AB. Xác định vị trí C để CK.AD+CE.DB có giá trị lớn nhất.
Nhờ mọi người giải dùm e với.

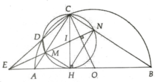
a, Tứ giác CMHN là hình chữ nhật
b, Ta có
O
C
A
^
=
O
A
C
^
C B A ^ = A C H ^ ; A C H ^ = C M N ^
=> O C A ^ + C M N ^ = 90 0
Vậy OC ⊥ MN
c, Ta có ∆IOC có E là trực tâm suy ra IN đi qua M và E (đpcm)
d, Ta có E M A ^ = C M N ^ ; C M N ^ = C B A ^ => ∆EMA:∆ENB
Tương tự ∆EMH:∆EHN => EM.EN = E H 2 ngoài ra , ∆EHC vuông tại H có HD là đường cao
=> E H 2 = ED.EC. Từ đó ta có đpcm