Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\overrightarrow{AM}+\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{AC}\)
b: \(=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}\)
\(=\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}\)
c: \(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CA}\)
\(=\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)=\overrightarrow{0}\)

Bài 1 và Bài 2 tương tự nhau nên mk sẽ chỉ CM bài 1 thôi nha
Có \(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\overrightarrow{AB}+\overrightarrow{CD}=0\)
\(\Rightarrow\overrightarrow{AD}+\overrightarrow{DB}+\overrightarrow{CB}+\overrightarrow{BD}=0\)
\(\Leftrightarrow\overrightarrow{AD}+\overrightarrow{CB}=0\Leftrightarrow\overrightarrow{AD}=\overrightarrow{BC}\)
Bài 3:
Xét \(\Delta AIP\) theo quy tắc trung điểm có:
\(\overrightarrow{IC}=\frac{\overrightarrow{IA}+\overrightarrow{IP}}{2}\)
Làm tương tự vs các tam giác còn lại
\(\Rightarrow\overrightarrow{IB}=\frac{\overrightarrow{IN}+\overrightarrow{IC}}{2}\)
\(\Rightarrow\overrightarrow{IA}=\frac{\overrightarrow{IB}+\overrightarrow{IM}}{2}\)
Cộng vế vs vế
\(\Rightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\frac{\overrightarrow{IA}+\overrightarrow{IP}+\overrightarrow{IN}+\overrightarrow{IC}+\overrightarrow{IB}+\overrightarrow{IM}}{2}\)
\(\Leftrightarrow2\overrightarrow{IA}+2\overrightarrow{IB}+2\overrightarrow{IC}=\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{IM}+\overrightarrow{IN}+\overrightarrow{IP}\)
\(\Leftrightarrow\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{IM}+\overrightarrow{IN}+\overrightarrow{IP}\left(đpcm\right)\)

Dựa theo đề bài ta có hình vẽ: A B C M N I
Ta có: MA = 2MB; BN = 5CN => BN = 5/6 BC
Có \(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}=-\overrightarrow{BA}+\frac{5}{6}\overrightarrow{BC}\)
Áp dụng định lí menelaus cho tam giác ABN
\(\frac{MA}{MB}.\frac{CB}{CN}.\frac{IN}{IA}=1\)=> \(\frac{2}{1}.\frac{6}{1}.\frac{IN}{IA}=1\Rightarrow IA=12IN\)=> \(\overrightarrow{AI}=\frac{12}{13}\overrightarrow{AN}\)
Ta có: \(\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{AI}=\overrightarrow{BA}+\frac{12}{13}\overrightarrow{AN}=\overrightarrow{BA}+\frac{12}{13}\left(-\overrightarrow{BA}+\frac{5}{6}\overrightarrow{BC}\right)\)rút gọn tính tiếp nhé
a) Nối BM
Ta có AM= AB.cosMAB
=> | | = |
| = | |.cos(
|.cos( ,
,  )
)
Ta có: .
.  = |
= | |.|
|.| | ( vì hai vectơ
| ( vì hai vectơ  ,
,  cùng phương)
cùng phương)
=> .
.  = |
= | |.|
|.| |.cosAMB.
|.cosAMB.
nhưng | |.|
|.| |.cos(
|.cos( ,
,  ) =
) =  .
.
Vậy .
.  =
=  .
.
Với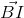 .
.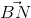 =
= 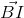 .
.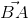 lý luận tương tự.
lý luận tương tự.
A B M N I
b)