Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

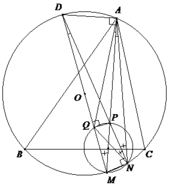
2) Tứ giác APQD nội tiếp ( P Q D ^ = M A D ^ = 90 0 ),
suy ra P A Q ^ = P D Q ^ = N D M ^ (3).
Xét (O), ta có N D M ^ = N A M ^ (4).
Từ (3) và (4) P A Q ^ = N A P ^ , suy ra AP là phân giác của góc N A Q ^ (*).
Xét (O), ta có A N D ^ = A M D ^ .
Xét đường tròn đường kính MP có Q M P ^ = Q N P ^ ⇒ A N P ^ = Q N P ^ , nên NP là phân giác của góc ANQ (**).
Từ (*) và (**), suy ra P là tâm đường tròn nội tiếp tam giác ANQ

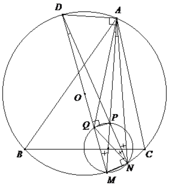
1). Vì MP là đường kính suy ra P N ⊥ M N (1).
Vì MD là đường kính suy ra D N ⊥ M N (2).
Từ (1) và (2), suy ra N; P; D thẳng hàng.

a) Xét tứ giác HMBI có:
∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AN}=\widebat{CN}\))
Mà 2 góc này cùng nhìn cạnh HI
=> Tứ giác BMHI nội tiếp
b) Xét ΔMNI và ΔMKC có:
∠KMC là góc chung
∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{BM}\))
=> ΔMNI ∼ ΔMCK => \(\frac{MN}{MC}=\frac{MI}{MK}\) => MN.MK = MC.MI
c) Xét tứ giác NKIC có:
∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{MB}\))
Mà 2 góc này cùng nhìn cạnh KI
=> Tứ giác NKIC là tứ giác nội tiếp
=> ∠NKI + ∠NCI = 180o (1)
Xét đường tròn (O) có:
\(\hept{\begin{cases}\widehat{ANK}=\widehat{ACM}\left(\text{2 góc nội tiếp cùng chắn cung AM}\right)\\\widehat{NAK}=\widehat{NCA}\left(\text{2 góc nội tiếp cùng chắn 2 cung BẰNG NHAU}\widebat{AN}=\widebat{CN}\right)\end{cases}}\)
=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)
Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180o (3)
Từ (1), (2), (3) => ∠NKI = ∠NKA
Xét tam giác IKN và tam giác AKN có:
∠NKI = ∠NKA
KN là cạnh chung
∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)
=> ΔIKN = ΔAKN
=> IK=AK =>ΔAKI cân tại K
Tứ giác NKIC là tứ giác nội tiếp
Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))
∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))
=> Tứ giác AHIK là hình bình hành
Mà IK = AK
=> Tứ giác AHIK là hình thoi.
CÒN LẠI TỰ LÀM LÀM NHA

a: Gọi H là trung điểm của CD
=>H là tâm đường tròn đường kính CD
Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA và OC là phân giác của góc MOA
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB và OD là phân giác của góc MOB
ta có: OC là phân giác của góc MOA
=>\(\hat{MOA}=2\cdot\hat{MOC}\)
ta có: OD là phân giác của góc MOB
=>\(\hat{MOB}=2\cdot\hat{MOD}\)
ta có: \(\hat{MOA}+\hat{MOB}=180^0\) (hai góc kề bù)
=>\(2\left(\hat{MOC}+\hat{MOD}\right)=180^0\)
=>\(2\cdot\hat{COD}=180^0\)
=>\(\hat{COD}=90^0\)
=>O nằm trên đường tròn đường kính CD
hay O nằm trên (H)
Xét hình thang ABDC có
O,H lần lượt là trung điểm của AB,CD
=>OH là đường trung bình của hình thang ABDC
=>OH//AC//BD và \(OH=\frac{AC+BD}{2}\)
ta có: OH//AC
CA⊥AB
Do đó: OH⊥AB
=>(H) tiếp xúc với AB tại O
b: \(C_{ABDC}=AC+CD+DB+AB\)
=CM+CD+DM+AB
=CD+CD+AB
=2CD+AB
Kẻ CK⊥BD tại K
=>CK<=CD
CK⊥BD
AB⊥BD
Do đó: CK//AB
Xét tứ giác ABKC có
KC//AB
AC//BK
Do đó: ABKC là hình bình hành
=>KC=AB=2R
Để chu vi hình thang ABDC nhỏ nhất thì 2CD+AB nhỏ nhất
mà AB cố định
nên 2CD nhỏ nhất
=>CD nhỏ nhất
mà CD<=CK=2R
nên CD nhỏ nhất khi CD=2R
mà OM=R
nên OM=1/2CD
ΔCOD vuông tại O
mà OH là đường trung tuyến
nên \(OH=\frac12CD\)
=>OM=OH
=>M trùng với H
=>MO⊥AB tại O
=>M là điểm chính giữa của cung AB
c: \(C_{ABDC}=2CD+AB\)
=>2CD+4=14
=>2CD=10
=>CD=5(cm)

Xét ΔOAI và ΔOBI có
OA=OB
OI chung
AI=BI
Do đó: ΔOAI=ΔOBI
Suy ra: \(\widehat{AOI}=\widehat{BOI}\)
hay OI là tia phân giác của góc xOy
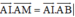 và
và 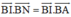
 theo R.
theo R.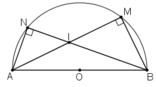

 | = |
| = | |.cos(
|.cos( ,
, 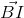 .
.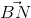 =
= 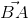 lý luận tương tự.
lý luận tương tự.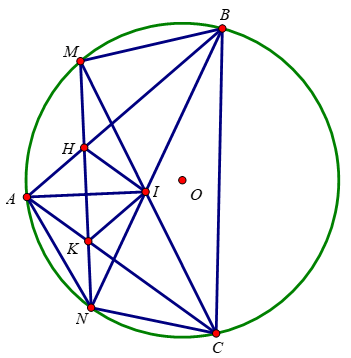

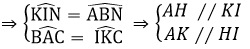
a) Nối BM
Ta có AM= AB.cosMAB
=> |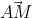 | = |
| = |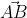 |.cos(
|.cos( ,
, 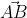 )
)
Ta có: .
. 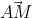 = |
= | |.|
|.|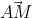 | ( vì hai vectơ
| ( vì hai vectơ  ,
, 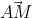 cùng phương)
cùng phương)
=> .
. 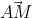 = |
= | |.|
|.|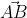 |.cosAMB.
|.cosAMB.
nhưng | |.|
|.|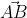 |.cos(
|.cos( ,
, 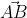 ) =
) =  .
.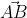
Vậy .
. 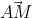 =
=  .
.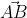
Với .
. =
=  .
. lý luận tương tự.
lý luận tương tự.
b) .
. 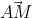 =
=  .
.![This...
</div>
<div class=]()