Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

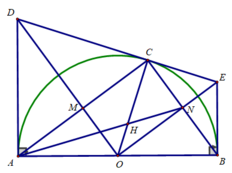
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC 2 = R 2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC 2 = R 2
Khi đó: OM.OD + ON.OE = 2 R 2
Vậy OM.OD + ON.OE không đổi

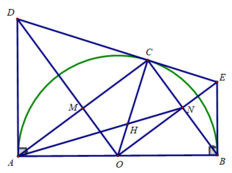
d) Ta có: N là trung điểm của BC
⇒ AN là trung tuyến của ΔABC
CO cũng là trung tuyến của ΔABC
AN ∩ CO = H
⇒ H là trọng tâm ΔABC
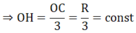
Vậy khi C di chuyển trên nửa đường tròn (O) thì H di chuyển trên nửa đường tròn
(O; R/3)

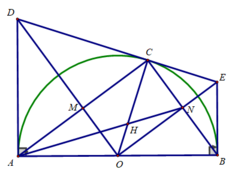
b) Xét tứ giác OMCN có:
∠(OMC) = 90 0 (AC ⊥ OD)
∠(ONC) = 90 0 (CB ⊥ OE)
∠(NCM) = 90 0 (AC ⊥ CB)
⇒ Tứ giác OMCN là hình chữ nhật

a: Xét (O) có
DA là tiếp tuyến có A là tiếp điểm
DC là tiếp tuyến có C là tiếp điểm
Do đó: DA=DC
Xét (O) có
EC là tiếp tuyến có E là tiếp điểm
EB là tiếp tuyến có B là tiếp điểm
Do đó: EC=EB
Ta có: CD+CE=DE
nên DA+EB=DE

a: Xét (O) có
DA,DE là các tiếp tuyến
=>DA=DE và OD là phân giác của góc AOE
OD là phân giác của góc AOE
=>\(\widehat{AOE}=2\cdot\widehat{DOE}\)
Xét (O) có
CE,CB là các tiếp tuyến
Do đó: CE=CB và OC là phân giác của góc EOB
OC là phân giác của góc EOB
=>\(\widehat{EOB}=2\cdot\widehat{EOC}\)
Ta có: \(\widehat{EOA}+\widehat{EOB}=180^0\)(hai góc kề bù)
=>\(2\left(\widehat{EOC}+\widehat{EOD}\right)=180^0\)
=>\(2\cdot\widehat{DOC}=180^0\)
=>\(\widehat{DOC}=90^0\)
Ta có: ΔOED vuông tại E
=>\(OE^2+ED^2=OD^2\)
=>\(ED^2+6^2=10^2\)
=>\(ED^2=100-36=64\)
=>\(ED=\sqrt{64}=8\left(cm\right)\)
Xét ΔODC vuông tại O có OE là đường cao
nên \(DE\cdot DC=DO^2\)
=>\(8\cdot DC=10^2=100\)
=>DC=100/8=12,5(cm)
Xét ΔDOE vuông tại E có \(sinDOE=\dfrac{DE}{DO}=\dfrac{4}{5}\)
nên \(\widehat{DOE}\simeq53^0\)
b: Gọi F là trung điểm của DC
Ta có: ΔDOC vuông tại O
mà OF là đường trung tuyến
nên OF=FD=FC
=>F là tâm đường tròn ngoại tiếp ΔDOC
Xét hình thang ABCD có
O,F lần lượt là trung điểm của AB,CD
=>OF là đường trung bình của hình thang ABCD
=>OF//AD//CB
Ta có: OF//AD
AD\(\perp\)AB
Do đó: FO\(\perp\)AB
=>AB là tiếp tuyến của (F)
=>AB là tiếp tuyến của đường tròn ngoại tiếp ΔODC

C là giao điểm 2 tiếp tuyến tại A và M \(\Rightarrow OC\) là trung trực AM
\(\Rightarrow E\) là trung điểm AM
Tương tự ta có OD là trung trực BM \(\Rightarrow F\) là trung điểm BM
\(\Rightarrow EF\) là đường trung bình tam giác ABM
\(\Rightarrow EF||AB\Rightarrow ONEF\) là hình thang (1)
Lại có O là trung điểm AB \(\Rightarrow OF\) là đường trung bình tam giác ABM
\(\Rightarrow OF=\dfrac{1}{2}AM=AE\)
Mà \(OF||AE\) (cùng vuông góc BM)
\(\Rightarrow AEFO\) là hình bình hành \(\Rightarrow\widehat{OFE}=\widehat{OAE}\)
Mà \(EN=AE=\dfrac{1}{2}AM\Rightarrow\Delta AEN\) cân tại E \(\Rightarrow\widehat{OAE}=\widehat{ANE}\)
\(\widehat{ANE}+\widehat{ONE}=180^0\Rightarrow\widehat{OFE}+\widehat{ONE}=180^0\)
Lại có \(\widehat{ONE}+\widehat{NEF}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{OFE}=\widehat{NEF}\)
\(\Rightarrow ONEF\) là hình thang cân

a: Xét (O) có
DC,DA là tiếp tuyến
=>DC=DA và OD là phân giác của góc COA
=>OD vuông góc AC
Xét (O) có
EC,EB là tiếp tuyến
=>EB=EC và OE là phân giác của góc COB(2)
=>OE là trung trực của BC
=>OE vuông góc CB
AD+BE=DC+CE=DE
b: Từ (1), (2) suy ra góc DOE=1/2*180=90 độ
Xét tứ giác CMON có
góc CMO=góc CNO=góc MON=90 độ
=>CMON là hình chữ nhật
c: OM*OD+ON*OE
=OC^2+OC^2
=2*R^2ko đổi
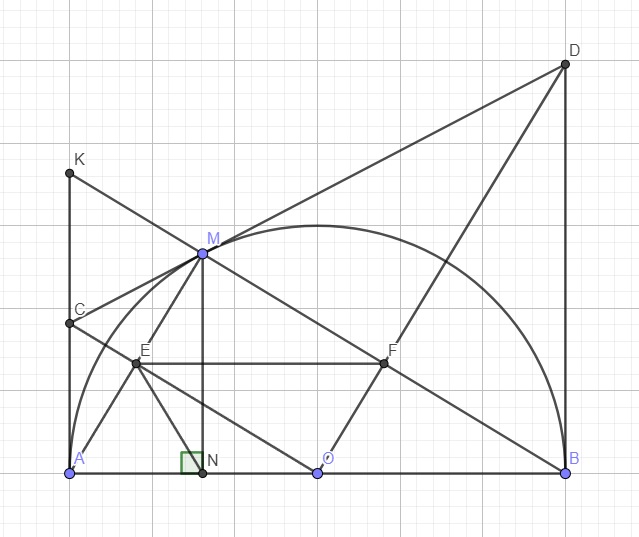
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE