Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HS tự chứng minh
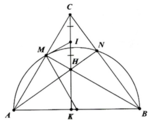
b, Gọi CH ∩ AB = K
Chứng minh được ∆MIC cân tại I
=> I C M ^ = I M C ^
Tương tự: O M A ^ = O A M ^
Chứng minh được I M O ^ = 90 0 => ĐPCM

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
=>ΔAMB vuông tại M
Xét (O) có
ΔANB nội tiếp
AB là đường kính
=>ΔANB vuông tại N
Xét ΔCAB có
AN.BM là đường cao
AN cắt BM tại H
=>H là trực tâm
=>CH vuông góc AB
b:
Gọi giao của CH vơi AB là K
=>CH vuông góc AB tại K
góc OMI=góc OMH+góc IMH
=góc OBM+góc IHM
=góc OBM+góc BHK=90 độ
=>IM là tiếp tuyến của (O)

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét (O) có
ΔANB nội tiếp
AB là đường kính
Do đó: ΔANB vuông tại N
Xét ΔCAB có
AN,BM là các đường cao
AN cắt BM tại H
Do đó: H là trực tâm
=>CH vuông góc với AB
b: góc IMO=góc IMH+góc OMH
=90 độ-góc ACH+góc ABM
=90 độ
=>MI là tiếp tuyến của (O)

a) Vì AH, HB, AB đều là các đường kính của các nửa đường tròn (O1) , (O2) và (O) nên tứ giác MPHQ có ba góc P, Q, M vuông. Vì vậy nó là hình chữ nhật.
Từ đó, ta có HM = PQ.
b) Vì MHPQ là hình chữ nhật nên \widehat{MPQ}=\widehat{MHQ}=\widehat{MBH}\left(=\dfrac{\stackrel\frown{HQ}}{2}\right)MPQ=MHQ=MBH(=2HQ⌢), do đó APQB là tứ giác nội tiếp.
c) Ta có \widehat{O_1PA}=\widehat{PAO_1}=90^o-\widehat{HMP}=90^o-\widehat{MPQ}O1PA=PAO1=90o−HMP=90o−MPQ
\Rightarrow\widehat{O_1PA}+\widehat{MPQ}=90^o\Rightarrow\widehat{O_1PQ}=90^o⇒O1PA+MPQ=90

bài làm
a, gọi H là tiếp điểm của tiếp tuyến MN
theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
nên ta có: MN=HM=HN=\(\dfrac{1}{2}\)(AOH =HON)=90 độ
vậy góc MON=90 đọ và là tâm giác vuông tại O đường cao OH
b,theo giả thuyết 2 tiếp tuyến AM và MH cắt nhau tại M
⇒ AM=MH ( tính chất 2 tiếp tuyến cắt nhau)
theo giả thuyết 2 tiếp tuyến HN cắt BN tại N
⇒ HN=BN ( tính chất 2 tiếp tuyến cắt nhau)
Theo hệ thức lượng trong tam giác vuông: OI^2=MI.INOH2=MH.HNAM.BN=MI.NI=OI^
Vì vậy AM.BN=MI.NI=OI^2=R^2AM.BN=MH.NH=
\(OH^2\)=\(R^2\)

(Quá lực!!!)
E N A B C D O H L
Đầu tiên, hãy CM tam giác \(EAH\) và \(ABD\) đồng dạng.
Từ đó suy ra \(\frac{EA}{AB}=\frac{AH}{BD}\) hay \(\frac{EA}{OB}=\frac{AC}{BD}\).
Từ đây CM được tam giác \(EAC\) và \(OBD\) đồng dạng.
Suy ra \(\widehat{ECA}=\widehat{ODB}\). Do đó nếu gọi \(OD\) cắt \(EC\) tại \(L\) thì CM được \(OD⊥EC\).
-----
Đường tròn đường kính \(NC\) cắt \(EC\) tại \(F\) nghĩa là \(NF⊥EC\), hay \(NF\) song song với \(OD\).
Vậy \(NF\) chính là đường trung bình của tam giác \(AOD\), vậy \(NF\) qua trung điểm \(AO\) (là một điểm cố định) (đpcm)



CH=2R =90
xét jfnfjdmemekekd