Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

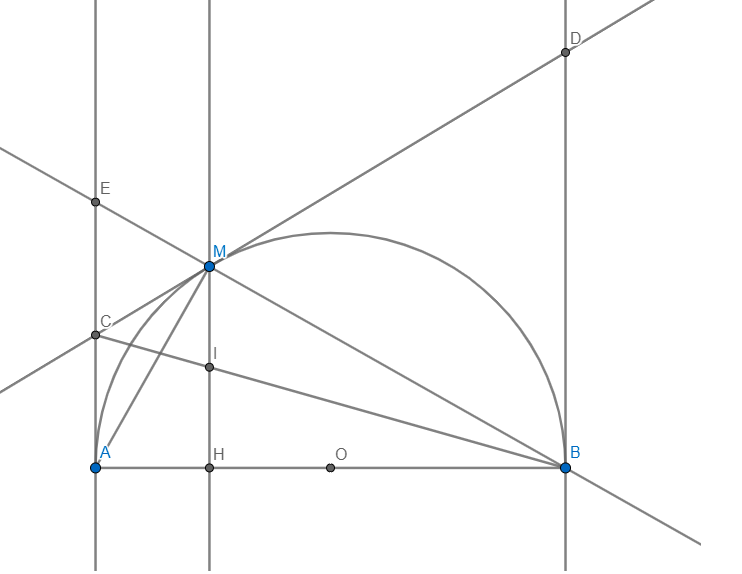
c) BM cắt Ax tại E.BC cắt MH tại I
Vì AB là đường kính nên \(\angle AMB=90\)
Vì CM,CA là tiếp tuyến nên \(CM=CA\)
Ta có tam giác AME vuông tại M có \(CM=CA\Rightarrow C\) là trung điểm AE
Vì \(MH\parallel AE(\bot AB)\) \(\Rightarrow\left\{{}\begin{matrix}\dfrac{IH}{AC}=\dfrac{BI}{BC}\\\dfrac{IM}{CE}=\dfrac{BI}{BC}\end{matrix}\right.\Rightarrow\dfrac{IH}{AC}=\dfrac{IM}{CE}\)
mà \(AC=CE\Rightarrow IH=IM\) nên ta có đpcm

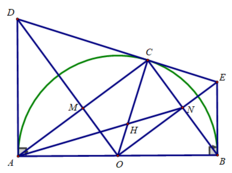
a) CE và EB là 2 tiếp tuyến cắt nhau tại E
⇒ EC = EB và CB ⊥ OE
Tương tự, DC và DA là 2 tiếp tuyến cắt nhau tại D
⇒ DC = DA và AC ⊥ OD
Khi đó: AD + BE = DC + EC = DE

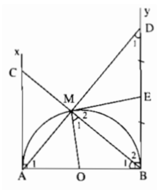
Tam giác EBM cân nên ∠ M 2 = ∠ B 2 . Suy ra ∠ M 1 + ∠ M 2 = ∠ B 1 + ∠ B 2 = 90 ° , tức là ME ⊥ OM tại M. Vậy ME là tiếp tuyến của nửa đường tròn.

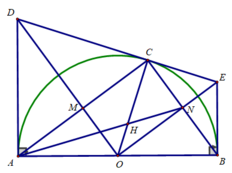
c) Xét tam giác DOC vuông tại C, CM là đường cao có:
OM.OD = OC 2 = R 2
Xét tam giác EOC vuông tại C, CN là đường cao có:
ON.OE = OC 2 = R 2
Khi đó: OM.OD + ON.OE = 2 R 2
Vậy OM.OD + ON.OE không đổi
a, Theo tính chất 2 tt cắt nhau: \(AC=CH;BD=DH\Rightarrow AC+BH=CH+HD=CD\)
b, Vì \(AC=CH;CO.chung;\widehat{CAO}=\widehat{CHO}=90^0\) nên \(\Delta CAO=\Delta CHO\left(cgv-ch\right)\)
Do đó \(\widehat{AOC}=\widehat{COH}\) hay OC là p/g \(\widehat{AOH}\)
Tương tự: \(\widehat{BOD}=\widehat{DOH}\) hay OD là p/g \(\widehat{HOB}\)
\(\Rightarrow\widehat{COD}=\widehat{COH}+\widehat{HOD}=\dfrac{1}{2}\left(\widehat{AOH}+\widehat{HOB}\right)=90^0\\ \Rightarrow\Delta OCD\perp O\)
Do đó OCD nội tiếp đường tròn tâm là trung điểm CD
Gọi I là trung điểm CD
Xét hthang ABDC(AC//BD) có O là trung điểm AB, I là trung điểm CD nên OI là đtb ht ABDC
\(\Rightarrow OI//AC\\ \Rightarrow OI\perp AB\)
Vậy AB là tt đường tròn nt tg OCD