Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. ta có: góc MAC = 900 (MA vuong góc AC)
góc MDC = 900 (MD vuong góc DC)
xét tứ giác ACDM co:
Góc MAC + góc MDC =90+90= 1800
tứ giác ACDM nội tiếp đường tròn ( tổng 2 góc đối bằng 1800)
2. ta có: góc ADB = 90 (góc nội tiếp chắn nửa đường tròn)
tam giác ADM vuông tại D
Góc DAB + DBA = 90
góc MAB = CMD ( 2 góc nội tiếp chắn nửa đường tròn)
góc DBA = DNC ( 2 góc nội tiếp chắn nửa đường tròn)
Góc CMD + góc DNC = 900
góc MNC = 900 Tam giác MNC vuông tại N

c) Gọi giao điểm của BM với Ax là I. Từ M kẻ MK vuông góc với AB. BC cắt MK tại E.
Vì MK vuông góc AB => MK // AC // BD
EK // AC => \(\frac{EK}{AC}=\frac{BE}{BC}\); ME // IC => \(\frac{ME}{IC}=\frac{BE}{BC}\) => \(\frac{EK}{AC}=\frac{ME}{IC}\)
Tam giác MIA vuông tại M có CA = CM => góc CAM = góc CMA => góc CIM = góc CMI => tam giác CMI cân tại C => CI = CM => CM = CI = CA => EK = ME.
\(EK=ME\Rightarrow\frac{EK}{BD}=\frac{ME}{BD}\)mà \(\frac{ME}{BD}=\frac{CM}{CD}=\frac{AK}{AB}\Rightarrow\frac{EK}{BD}=\frac{AK}{AB}\)
=> Tam giác AKE đồng dạng với tam giác ABD (c.g.c) => góc EAK = góc DAK => A,E,D thẳng hàng => BC cắt AD tại E mà theo giả thiết BC cắt AD tại N => E trùng với N => H trùng với K => N là trung điểm MH.

a) góc HEC = góc CAM = góc CBH.
b) CM EB2 = EC.EA = EM2 từ đó ta có góc EMC = góc EAM = góc ADC suy ra AD song song MB. Do đó góc BDA = góc ABM = góc BAD.
c) Ta có BJ là đường kính và BJ vuông góc với AD tại K (AD song song MB). Do đó KD = KA

viết đề sai rùi bạn
b) chứng minh tứ giác POMQ LÀ hình chữ nhật chứ ko phải chứng minh AQMO LÀ HÌNH CHỮ NHẬT OK

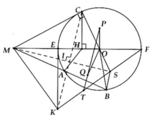
a, HS tự chứng minh
b, MH.MO = MA.MB ( = M C 2 )
=> ∆MAH:∆MOB (c.g.c)
=> M H A ^ = M B O ^
M B O ^ + A H O ^ = M H A ^ + A H O ^ = 180 0
=> AHOB nội tiếp
c, M K 2 = ME.MF = M C 2 Þ MK = MC
∆MKS = ∆MCS (ch-cgv) => SK = SC
=> MS là đường trung trực của KC
=> MS ^ KC tại trung của CK
d, Gọi MS ∩ KC = I
MI.MS = ME.MF = M C 2 => EISF nội tiếp đường tròn tâm P Þ PI = PS. (1)
MI.MS = MA.MB (= M C 2 ) => AISB nội tiếp đường tròn tâm Q Þ QI = QS. (2)
Mà IT = TS = TK (do DIKS vuông tại I). (3)
Từ (1), (2) và (3) => P, T, Q thuộc đường trung trực của IS => P, T, Q thẳng hàng