Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

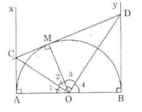
Ta có: AC = CM, BD = DM nên AC.BD = CM.MD
ΔCOD vuông tại O, ta có:
CM.MD = OM2 = R2 (R là bán kính đường tròn O).
Vậy AC.BD = R2 (không đổi).

a: Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB
Xét ΔNCA và ΔNBD có
\(\hat{NCA}=\hat{NBD}\) (hai góc so le trong, AC//BD)
\(\hat{CNA}=\hat{BND}\) (hai góc đối đỉnh)
Do đó: ΔNCA~ΔNBD
=>\(\frac{NC}{NB}=\frac{NA}{ND}=\frac{CA}{BD}=\frac{CM}{MD}\)
Xét ΔCDB có \(\frac{CM}{MD}=\frac{CN}{NB}\)
nên MN//DB
mà DB⊥AB
nên MN⊥AB
b: Gọi K là giao điểm của BM và AC
Ta có: MN⊥AB
AC⊥BA
Do đó: MN//AC
=>MH//AK
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM⊥MB
=>AM⊥MK tại M
=>ΔAMK vuông tại M
ta có: \(\hat{CMA}+\hat{CMK}=\hat{AMK}=90^0\)
\(\hat{CAM}+\hat{CKM}=90^0\) (ΔAMK vuông tại M)
mà \(\hat{CMA}=\hat{CAM}\) (ΔCAM cân tại C)
nên \(\hat{CMK}=\hat{CKM}\)
=>CM=CK
mà CM=CA
nên CK=CA(1)
Xét ΔBAC có NH//AC
nên \(\frac{NH}{AC}=\frac{BN}{BC}\left(2\right)\)
Xét ΔBCK có MN//CK
nên \(\frac{MN}{CK}=\frac{BN}{BC}\left(3\right)\)
Từ (1),(2),(3) suy ra NH=MN

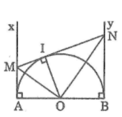
Tam giác OMN vuông tại O có OI ⊥ MN (tính chất tiếp tuyến)
Theo hệ thức lượng trong tam giác vuông, ta có:
O I 2 = MI.NI
Mà: MI = MA, NI = NB (chứng minh trên)
Suy ra : AM.BN = O I 2 = R 2

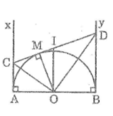
Theo tính chất tiếp tuyến, ta có:
Ax ⊥ AB
By ⊥ AB
Suy ra: Ax // By hay AC // BD
Suy ra tứ giác ABDC là hình thang
Gọi I là trung điểm của CD
Khi đó OI là đường trung bình của hình thang ABDC
Suy ra: OI // AC ⇒ OI ⊥ AB
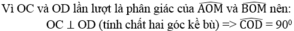
Suy ra: IC = ID = IO = (1/2).CD (tính chất tam giác vuông)
Suy ra I là tâm đường tròn đường kính CD. Khi đó O nằm trên đường tròn tâm I đường kính CD và IO vuông góc với AB tại O.
Vậy đường tròn có đường kính CD tiếp xúc với AB tại O.

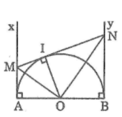
Ta có: MA = MI (tính chất hai tiếp tuyến cắt nhau)
NB = NI (tính chất hai tiếp tuyến cắt nhau)
Mà: MN = MI + IN
Suy ra: MN = AM + BN
Câu này hơi kì, vì đề đã nói rõ tiếp tuyến cắt Oz tại M, thế thì M chạy trên tia Oz còn hỏi gì nữa???
mình nghĩ câu này, nên "giấu" cái Oz đi, mà cho M là trung điểm của CD, làm thế nhé
Thấy tứ giác ABDC là hình thang vuông, có OM là đường trung bình (qua trung điểm 2 cạnh bên)
=> OM // Ax // By => M chạy trên tia qua O và // Ax (chính là Oz)
mơn bạn nha