Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
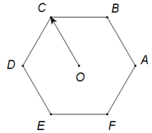
Các vecto cùng phương với ![]() có điểm đầu và điểm cuối là các đỉnh của lục giác :
có điểm đầu và điểm cuối là các đỉnh của lục giác : ![]()

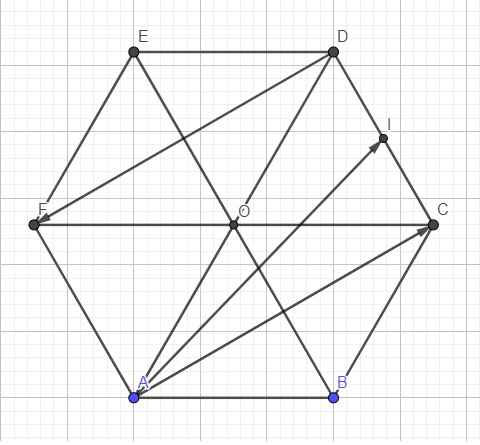
Số vecto khác vecto 0, có điểm đầu điểm cuối lấy từ 7 điểm A,B,C,D,E,F,O là:
\(A^2_7=7\cdot6=42\left(vecto\right)\)

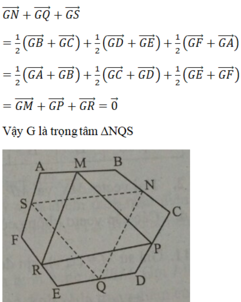
\(T=\left|\overrightarrow{DF}\right|=\left|\overrightarrow{DE}+\overrightarrow{EF}\right|\Rightarrow T^2=DE^2+EF^2+\overrightarrow{DE}.\overrightarrow{EF}\)
\(=a^2+a^2+a.a.cos60^0=3a^2\)
\(\Rightarrow\left|\overrightarrow{DF}\right|=a\sqrt{3}\)
\(AC=FD\Rightarrow\left|\overrightarrow{AC}\right|=a\sqrt{3}\)
\(P=\left|\overrightarrow{AI}\right|=\left|\dfrac{1}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AC}\right|\Rightarrow P^2=\dfrac{1}{4}\left(AD^2+AC^2+2\overrightarrow{AD}.\overrightarrow{AC}\right)\)
\(=\dfrac{1}{4}\left(4a^2+3a^2+2.2a.a\sqrt{3}.cos30^0\right)=\dfrac{11}{2}a^2\)
\(\Rightarrow\left|\overrightarrow{AI}\right|=\dfrac{a\sqrt{22}}{2}\)

Vì O là tâm của ngũ giác abcde nên O cũng là trọng tâm của ngũ giác nên vecto oa+ob+oc+od+oe=0

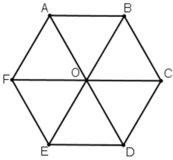
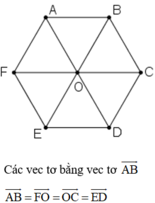
a) Các vectơ khác vectơ O→ và cùng phương với vectơ OA→ là:
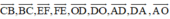
b) Các vectơ bằng vectơ AB→ là:

TenAnh1
TenAnh1
A = (-4.3, -5.94)
A = (-4.3, -5.94)
A = (-4.3, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
B = (11.06, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
D = (10.84, -5.94)
Các véc tơ bằng véc tơ \(\overrightarrow{AB}\) là:
\(\overrightarrow{OC};\overrightarrow{FO};\overrightarrow{ED}\).
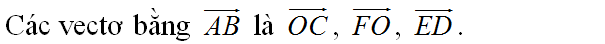
Ngũ giác đều chứ nhỉ ._?
Các vector bằng nhau: `\vec(AB) =\vec(ED) ; \vec(BA)=\vec(DE) ; \vec(BC)=\vec(FE) ; \vec(CB)=\vec(EF) ; \vec(AF)=\vec(CD) ; \vec(FA)=\vec(DC) ; \vec(AO)=\vec(OD) ; \vec(OA) =\vec(DO) ; \vec(BO)=\vec(OE) ; \vec(OB)=\vec(EO) ; \vec(FO)=\vec(OC) ; \vec(OF)=\vec(CO)`
Lục giác chứ ;-;