Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)
Với \(n=1\).
\(n^5-n=1^5-1=0\).
Do 0 chia hết cho 5 nên điều cần chứng minh đúng với n = 1.
Giả sử điều cần chứng minh đúng với \(n=k\).
Nghĩa là: \(k^5-k⋮5\).
Ta cần chứng minh nó đúng với \(n=k+1\).
Nghĩa là: \(\left(k+1\right)^5-\left(k+1\right)⋮5\).
Thật vậy:
\(\left(k+1\right)^5-\left(k+1\right)=C^0_5k^0+C^1_5k+...+C^5_5k^5-k-1\)
\(=1+C^1_5k+...+k^5-k-1\)
\(=C^1_5k+...+C^4_5k^4+k^5-k\)
Do mỗi \(C_5^1;C^2_5;C^3_5;C^4_5\) đều chia hết cho 5 và do gải thiết quy nạp \(k^5-k⋮5\) nên \(C^1_5k+...+C^4_5k^4+k^5-k\) chia hết cho 5.
Vì vậy: \(\left(k+1\right)^5-\left(k+1\right)⋮5\).
Vậy điều phải chứng minh đúng với mọi n.
b)
Tổng bình phương 3 số tự nhiên liên tiếp là: \(n^3+\left(n+1\right)^3+\left(n+2\right)^3\).
Ta cần chứng minh \(n^3+\left(n+1\right)^3+\left(n+2\right)^3⋮9,\forall n\in N^{\circledast}\).
Với n = 1.
\(n^3+\left(n+1\right)^3+\left(n+2\right)^3=1^3+2^3+3^3=36\).
Vậy điều cần chứng minh đúng với \(n=1\).
Giả sử điều cần chứng minh đúng với n = k.
Nghĩa là: \(k^3+\left(k+1\right)^3+\left(k+2\right)^3⋮9\).
Ta cần chứng minh nó đúng với \(n=k+1\).
Nghĩa là: \(\left(k+1\right)^3+\left(k+2\right)^3+\left(k+3\right)^3⋮9\)
Thật vậy:
\(\left(k+1\right)^3+\left(k+2\right)^3+\left(k+3\right)^3\)\(=\left(k+1\right)^3+\left(k+2\right)^3+k^3+3.3k^2+3.k.3^2+3^3\)
\(=\left(k+1\right)^3+\left(k+2\right)^3+k^3+9k^2+27k+81\)
Theo giả thiết quy nạp \(k^3+\left(k+1\right)^3+\left(k+2\right)^3⋮9\) và \(9k^2+27k+81=9\left(k^2+3k+9\right)⋮9\).
Nên \(\left(k+1\right)^3+\left(k+2\right)^3+k^3+9k^2+27k+81⋮9\).
Vậy điều phải chứng minh đúng với mọi n.
Bài 1:
\(\left(x^{-\frac{1}{5}}+x^{\frac{1}{3}}\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^k\left(x^{-\frac{1}{5}}\right)^k\left(x^{\frac{1}{3}}\right)^{10-k}=\sum\limits^{10}_{k=0}C_{10}^kx^{\frac{10}{3}-\frac{8k}{15}}\)
Trong khai triển trên có 11 số hạng nên số hạng đứng giữa có \(k=6\)
\(\Rightarrow\) Số hạng đó là \(C_{10}^6x^{\frac{10}{3}-\frac{48}{15}}=C_{10}^6x^{\frac{2}{15}}\)
Bài 2:
\(\left(1+x^2\right)^n=a_0+a_1x^2+a_2x^4+...+a_nx^{2n}\)
Cho \(x=1\Rightarrow2^n=a_0+a_1+...+a_n=1024=2^{10}\)
\(\Rightarrow n=10\)
\(\left(1+x^2\right)^{10}=\sum\limits^{10}_{k=0}C_{10}^kx^{2k}\)
Số hạng chứa \(x^{12}\Rightarrow2k=12\Rightarrow k=6\) có hệ số là \(C_{10}^6\)
Bài 3:
\(\left(x-\frac{1}{4}\right)^n=\sum\limits^n_{k=0}C_n^kx^k\left(-\frac{1}{4}\right)^{n-k}\)
Với \(k=n-2\Rightarrow\) hệ số là \(C_n^{n-2}\left(-\frac{1}{4}\right)^2=\frac{1}{16}C_n^2\)
\(\Rightarrow\frac{1}{16}C_n^2=31\Rightarrow C_n^2=496\Rightarrow n=32\)
Bài 4:
Xét khai triển:
\(\left(1+x\right)^n=C_n^0+xC_n^1+x^2C_n^2+...+x^nC_n^n\)
Cho \(x=2\) ta được:
\(\left(1+2\right)^n=C_n^0+2C_n^1+2^2C_n^2+...+2^nC_n^n\)
\(\Rightarrow S=3^n\)
Bài 5:
Xét khai triển:
\(\left(1+x\right)^n=C_n^0+xC_n^1+x^2C_n^2+...+x^{2k}C_n^{2k}+x^{2k+1}C_n^{2k+1}+...\)
Cho \(x=-1\) ta được:
\(0=C_n^0-C_n^1+C_n^2-C_n^3+...+C_n^{2k}-C_n^{2k+1}+...\)
\(\Rightarrow C_n^0+C_n^2+...+C_n^{2k}+...=C_n^1+C_n^3+...+C_n^{2k+1}+...\)
Bài 6:
\(\left(1-4x+x^2\right)^5=\sum\limits^5_{k=0}C_5^k\left(-4x+x^2\right)^k=\sum\limits^5_{k=0}\sum\limits^k_{i=0}C_5^kC_k^i\left(-4\right)^ix^{2k-i}\)
Ta có: \(\left\{{}\begin{matrix}2k-i=5\\0\le i\le k\le5\\i;k\in N\end{matrix}\right.\) \(\Rightarrow\left(i;k\right)=\left(1;3\right);\left(3;4\right);\left(5;5\right)\)
Hệ số: \(\left(-4\right)^1.C_5^3C_3^1+\left(-4\right)^3C_5^4.C_4^3+\left(-4\right)^5C_5^5.C_5^5\)
Đặt \(\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+....+\frac{1}{n\left(n+1\right)}=A\)
\(\Leftrightarrow A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+....+\frac{1}{n}-\frac{1}{n+1}\)
\(\Leftrightarrow A=\frac{n+1}{n+1}-\frac{1}{n+1}=\frac{n}{n+1}\)
Chẳng nhẽ không được chọn 
Đặt \(A=\frac{11}{n-2}.\frac{n}{7}=\frac{11n}{\left(n-2\right).7}=\frac{11n}{7n-14}\)
Để \(\frac{11n}{7n-14}\) có GTN thì 11n phải chia hết cho 7n-14
=>77n chia hết cho 7n-14 (1)
Ta lại có:
7n-14 chia hết cho 7n-14
=> 11(7n-14) chia hết cho 7n-14
=> 77n - 154 chia hết cho 7n-14 (2)
Trừ (1) cho (2) ta đc:
(77n) - (77n - 154) chia hết cho 7n-14
=> 154 chia hết cho 7n-14
\(\Rightarrow7n-14\inƯ\left(154\right)\)
\(\Rightarrow7n-14\in\left\{1;-1;2;-2;7;-7;11;-11\right\}\)
\(\Rightarrow7n\in\left\{15;13;16;12;21;7;25;3\right\}\)
\(\Rightarrow n\in\left\{3;2\right\}\)
Vậy n = 3 hoặc n = 2
Tốn công lắm nha !
a) Dễ thấy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
3k > 3k + 1
Nhân hai vế của (1) vơi 3, ta được:
3k + 1 > 9k + 3 <=> 3k + 1 > 3k + 4 + 6k -1.
Vì 6k - 1 > 0 nên
3k + 1 > 3k + 4 hay 3k + 1 > 3(k + 1) + 1.
tức là bất đẳng thức đúng với n = k + 1.
Vậy 3n > 3n + 1 với mọi số tự nhiên n ≥ 2.
b) Với n = 2 thì vế trái bằng 8, vế phải bằng 7. Vậy bất đẳng thức đúng với n = 2
Giả sử bất đẳng thức đúng với n = k ≥ 2, tức là
2k + 1 > 2k + 3 (2)
Ta phải chứng minh nó cũng đúng với n= k + 1, nghĩa là phải chứng minh
2k + 2 > 2(k + 1) + 3 <=> 2k + 2 > 2k + 5
Nhân hai vế của bất đẳng thức (2) với 2, ta được:
2k + 2 > 4k + 6 <=> 2k + 2 > 2k +5 + 2k + 1.
Vì 2k + 1> 0 nên 2k + 2 > 2k + 5
Vậy 2n + 1 > 2n + 3 với mọi số tự nhiên n ≥ 2.
a) Ta có:
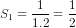
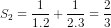
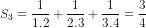
b) Từ câu a) ta dự đoán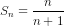 
(1), với mọi n ε N* .
Ta sẽ chứng minh đẳng thức (1) bằng phương pháp quy nạp
Khi n = 1, vế trái là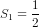 
, vế phải bằng 
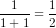. Vậy đẳng thức (1) đúng.
Giả sử đẳng thức (1) đúng với n = ≥ 1, tức là
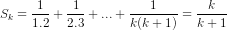
Ta phải chứng minh nó cũng đúng khi n = k + 1, nh=ghĩa là phải chứng minh
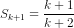
Ta có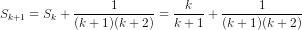 
= 
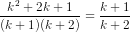
tức là đẳng thức (1) cũng đúng với n = k + 1.
Vậy điều cần chứng minh đúng với mọi n.
Phân tích nhân tử nhầm=>giải lại
\(A=2n^2-3n^2+n=n\left(2n^2-3n+1\right)=n\left(n-1\right)\left(2n+1\right)\)\(A=n\left(n-1\right)\left(2n+2-3\right)=\left[2n\left(n-1\right)\left(n+1\right)\right]-3\left(n\right)\left(n-1\right)=2B-3C\)
\(\left\{{}\begin{matrix}B⋮3\\C⋮2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2B⋮6\\3C⋮3\end{matrix}\right.\) \(\Rightarrow A⋮6\) => dpcm
Lời giải:
\(A=n\left(2n^3-3n+1\right)=n\left(n-1\right)\left(2n^2+2n-1\right)\)
\(A=n\left(n-1\right)\left[2n\left(n+1\right)-1\right]=2n\left(n-1\right)\left(n+1\right)+n\left(n-1\right)=B-C\)\(\left\{{}\begin{matrix}B⋮2\\B⋮3\end{matrix}\right.\)\(\Rightarrow B⋮6\forall n\in N\)
\(C=n\left(n-1\right)\) không thể chia hết cho 6 với mọi n thuộc N
\(\Rightarrow A\) chỉ chia hết cho 6 với điều kiện \(n\ne3k+2\)
ví dụ đơn giải với k=0 => n= 2
\(A=2.2^3-3.2^2+2=14⋮̸6\)
Kết luận đề sai
Trước tiên ta có một bổ đề sau:
Bổ đề: Cho 2 số \(a,b\) sao cho cả \(a,b\) đều viết được dưới dạng tổng của 4 số chính phương. Khi đó tích \(p=ab\) cũng có thể biểu diễn được thành tổng của 4 số chính phương.
\(\left(a_1^2+a_2^2+a_3^2+a_4^2\right)\left(b_1^2+b_2^2+b_3^2+b_4^2\right)\)
\(=\left(a_1b_1-a_2b_2-a_3b_3-a_4b_4\right)^2+\left(a_1b_2+a_2b_1+a_3b_4-a_4b_3\right)^2\) \(+\left(a_1b_3-a_2b_4+a_3b_1+a_4b_2\right)^2+\left(a_1b_4+a_2b_3-a_3b_2+a_4b_1\right)^2\)
Chứng minh thì bạn khai triển ra thôi.
Ta thấy \(0=0^2+0^2+0^2+0^2\)
\(1=0^2+0^2+0^2+1^2\)
\(2=0^2+0^2+1^2+1^2\)
Từ bổ đề trên, ta thấy chỉ cần chứng minh khẳng định đúng với số nguyên tố lẻ \(p\) thì coi như bài toán hoàn tất.
(Vì mọi số tự nhiên đều có thể viết được dưới dạng \(2^n.t\) với \(t\) lẻ)
Ta có số dư của \(a^2\) khi chia cho \(p\) luôn phân biệt khi cho \(a\) chạy từ \(0\) đến \(\dfrac{p-1}{2}\). Thật vậy, chọn \(a\) bất kì và đặt \(c=a^2modp\) \(\Rightarrow a\) là nghiệm của đa thức \(x^2-c\) trên trường \(Z/pZ\). Tương tự với \(p-a\left(\ne a\right)\). Ta biết rằng trong một trường \(K\), bất kì đa thức bậc \(n\) nào cũng chỉ có tối đa \(n\) nghiệm. Vì vậy không còn \(a\) nào khác là nghiệm của \(x^2-c\) nữa. Điều này có nghĩa là với mỗi số \(i\) trong tập hợp \(\left\{0,1,...,\dfrac{p-1}{2}\right\}\) thì tồn tại duy nhất \(a\) để \(a^2\equiv i\left[p\right]\)
Tương tự, khi \(b\) chạy từ tập \(\left\{0,1,...,\dfrac{p-1}{2}\right\}\) thì \(-b^2-1\) phân biệt. Áp dụng nguyên lí Dirichlet, tồn tại \(a,b\) sao cho \(a^2\equiv-b^2-1\left[p\right]\) \(\Leftrightarrow a^2+b^2+1^2+0^2=np\) với \(n\inℕ\)
Gọi \(m\) là số tự nhiên nhỏ nhất để \(mp\) là tổng của 4 số chính phương, \(x_1^2+x_2^2+x_3^2+x_4^2\). Ta chứng minh bằng phản chứng rằng \(m=1\) . Giả sử \(m\ne1\). Ta sẽ chỉ ra mâu thuẫn bằng việc chứng minh tồn tại một số tự nhiên \(r< m\) mà \(rp\) là tổng của 4 số chính phương.
Với mỗi \(x_i\) và \(y_i\) có cùng số dư khi chia cho \(m\) và nằm giữa \(\dfrac{-m+1}{2}\) và \(\dfrac{m}{2}\), ta có \(y_1^2+y_2^2+y_3^2+y_4^2=mr\), với \(0< r< m\)
Áp dụng bổ đề, ta có \(mpmr=z_1^2+z_2^2+z_3^2+z_4^2\). Vì \(x_i\equiv y_i\left[m\right]\) nên \(z_i⋮m\). Thật vậy:
\(z_1=x_1y_1+x_2y_2+x_3y_3+x_4y_4\) \(\equiv x_1^2+x_2^2+x_3^2+x_4^2\) \(\equiv mp\equiv0\left[m\right]\)
\(z_2=x_1y_2-x_2y_1+x_3y_4-x_4y_3\equiv x_1x_2-x_2x_1+x_3x_4-x_4x_3\equiv0\left[m\right]\)
Bằng cách tương tự chứng minh được \(z_3,z_4⋮m\)
Vậy với \(w_i=\dfrac{z_i}{m}\) thì \(w_1^2+w_2^2+w_3^2+w_4^2=rp\), điều này mâu thuẫn với tính nhỏ nhất của \(m\).
(Ta loại TH \(y_1=y_2=y_3=y_4=\dfrac{m}{2}\), khi đó \(r=m\); và TH \(y_1=y_2=y_3=y_4=0\), khi đó \(r=0\) vì cả 2 TH này đều cho ra \(mp=x_1^2+x_2^2+x_3^2+x_4^2⋮m^2\), vô lí vì \(p\) là số nguyên tố lớn hơn \(m\))
Do vậy điều giả sử là sai \(\Rightarrow\) đpcm.