
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

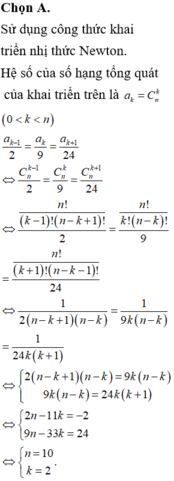

Đáp án là C. Ta có a,b∈N* không suy ra a -1, b -1∈N* . Do vậy không áp dụng được giả thiết quy nạp cho cặp {a -1, b -1}.
Chú ý: nêu bài toán trên đúng thì ta suy ra mọi số tự nhiên đều bằng nhau. Điều này là vô lí.

\(a,u_1+u_n=u_1+\left[u_1+\left(n-1\right)d\right]=u_1+u_1+\left(n-1\right)d=2u_1+\left(n-1\right)d\\ u_2+u_{n-1}=\left[u_1+d\right]+\left[u_1+\left(n-2\right)d\right]=2u_1+\left(n-1\right)d\\ ...\\ u_k+u_{n-k+1}=\left[u_1+\left(k-1\right)d\right]+\left[u_1+\left(n-k+1-1\right)d\right]=2u_1+\left(n-1\right)d\)
\(b,u_1+u_n=2u_1+\left(n-1\right)d\\ u_2+u_{n-1}=2u_1+\left(n-1\right)d\\ ...\\ u_n+u_1=2u_1+\left(n-1\right)d\)
Cộng vế với vế, ta được:
\(2\left(u_1+u_2+...+u_n\right)=n\left[2u_1+\left(n-1\right)d\right]\\ \Leftrightarrow2\left(u_1+u_2+...+u_n\right)=n\left(u_1+u_n\right)\)

Chọn $k$ đồ vật cùng lúc trong $n$ đồ vật thì chọn A.
Chọn $k$ đồ vật lần lượt thì sẽ chọn đáp án B như bạn nói. Lý giải:
Chọn lần 1, có $n$ cách chọn
Chọn lần 2, có $n-1$ cách chọn
.....
Chọn lần $k$, có $n-k+1$ cách chọn
Số cách chọn: $n(n-1)...(n-k+1)=\frac{n!}{(n-k)!}=A^k_n$

f' (a) =6a +5 -[(2k+1)a^2k +6k a^(2k-1) +(k+1)a^k +3k a^k ]
f'(1) =6+5-[(2k+1)+6k+(k+1) +3k]
f'(1) =11-(12k+2)=9-12k
mình biết lâu rôi (4 tháng)
mình cũng chưa hiểu vấn đề này
chỉ biết
\(y=x^{\alpha}\Rightarrow y'=\alpha x^{\alpha-1}\) vì sao nó vậy thực sự mình cũng chẳng biết (cứ chấp nhận nó đúng vậy thôi)
mình cứ cho nó đúng từ đó nội suy ra cái khác
p/s
trước sau gì tìm hiểu sâu để biết --> hiện tai chưa
