Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\dfrac{C_n^k}{\left(k+1\right)\left(k+2\right)}=\dfrac{n!}{\left(k+1\right)\left(k+2\right).k!\left(n-k\right)!}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}.\dfrac{\left(n+2\right)!}{\left(n+2-\left(k+2\right)\right)!\left(k+2\right)!}\)
\(=\dfrac{1}{\left(n+1\right)\left(n+2\right)}.C_{n+2}^{k+2}\)
Đặt tổng trên là A
\(\Rightarrow A=\dfrac{-1.C_{2024}^3}{2023.2024}+\dfrac{2.C_{2024}^4}{2023.2024}+\dfrac{-3.C_{2024}^5}{2023.2024}+...+\dfrac{2022.C_{2024}^{2024}}{2023.2024}\)
\(=\dfrac{1}{2023.2024}\left(-1.C_{2024}^3+2.C_{2024}^4+...+2022.C_{2024}^{2024}\right)=\dfrac{1}{2023.2024}.B\)
Xét \(C=-2.\left(-C_{2024}^3+C_{2024}^4-C_{2024}^5+...+C_{2024}^{2024}\right)\)
\(\Rightarrow B-C=-3C_{2024}^3+4C_{2024}^4-5C_{2024}^5+...+2024.C_{2024}^{2024}\)
Ta có:
\(k.C_n^k=\dfrac{n!.k}{\left(n-k\right)!.k!}=n.\dfrac{\left(n-1\right)!}{\left(\left(n-1\right)-\left(k-1\right)\right)!.\left(k-1\right)!}=n.C_{n-1}^{k-1}\)
\(\Rightarrow B-C=-2024.C_{2023}^2+2024C_{2023}^3+...+2024.C_{2023}^{2023}\)
\(=-2024\left(C_{2023}^2-C_{2023}^3+...-C_{2023}^{2023}\right)\)
Xét khai triển:
\(\left(1-x\right)^k=C_k^0-xC_k^1+x^2C_k^2+...+\left(-1\right)^kx^k.C_k^k\)
Thay \(k=2024\); \(x=1\)
\(\Rightarrow0=C_{2024}^0-C_{2024}^1+C_{2024}^2-C_{2024}^3+...+C_{2024}^{2024}\)
\(\Rightarrow-C_{2024}^3+...+C_{2024}^{2024}=C_{2024}^1-C_{2024}^2-1\)
\(\Rightarrow C=-2\left(C_{2024}^1-C_{2024}^2-1\right)=-2\left(2023-C_{2024}^2\right)\)
Thay \(k=2023;x=1\)
\(\Rightarrow0=C_{2023}^0-C_{2023}^1+C_{2023}^2+...-C_{2023}^{2023}\)
\(\Rightarrow C_{2023}^2-C_{2023}^3+...-C_{2023}^{2023}=C_{2023}^1-1=2022\)
\(\Rightarrow B-C=-2024.2022\)
\(\Rightarrow B=C-2022.2024=-2\left(2023-C_{2024}^2\right)-2022.2024\)
\(=-2.2023+2023.2024-2022.2024\)
\(=-2022\)
\(\Rightarrow A=\dfrac{-2022}{2023.2024}\)
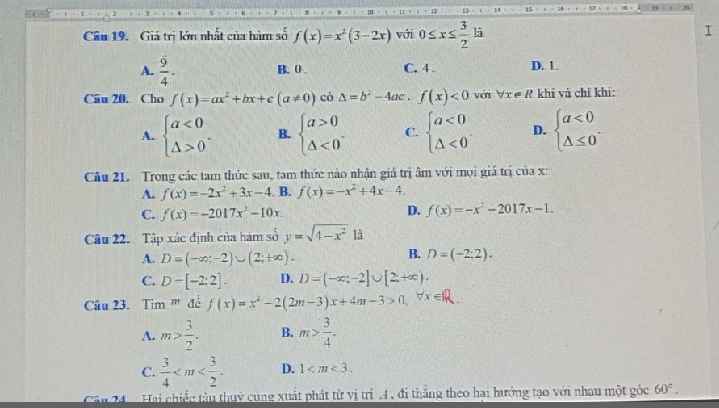
19.
\(f\left(x\right)=x^2\left(3-2x\right)=x.x.\left(3-2x\right)\le\left(\dfrac{x+x+3-2x}{3}\right)^3=1\)
\(\Rightarrow\max\limits_{\left[0;\dfrac{3}{2}\right]}f\left(x\right)=1\)
20.
\(f\left(x\right)< 0;\forall x\in R\Leftrightarrow\left\{{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\)
21.
A là đáp án đúng, do đa thức \(f\left(x\right)=-2x^2+3x-4\) có:
\(\left\{{}\begin{matrix}a=-2< 0\\\Delta=3^2-4.\left(-2\right).\left(-4\right)=-23< 0\end{matrix}\right.\)
22.
ĐKXĐ: \(4-x^2\le0\Rightarrow\left(2-x\right)\left(2+x\right)\le0\)
\(\Rightarrow-2\le x\le2\Rightarrow D=\left[-2;2\right]\)
23.
\(f\left(x\right)>0;\forall x\Leftrightarrow\left\{{}\begin{matrix}a=1>0\\\Delta'=\left(2m-3\right)^2-\left(4m-3\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow4m^2-16m+12< 0\)
\(\Rightarrow1< m< 3\)
Theo Vi-ét ta có:
△' = (m+1)2 -m(m-2)
△' = 1 >0
Vậy pt luôn có nghiệm ∀m
giải chi tiết giúp mình với ạ
Ta có: \(x^2-6x+m-2=0\)
\(\Rightarrow\Delta=6^2-4\left(m-2\right)\)
Để phương tình có hai nghiệm phân biệt thì \(\Delta>0\)
\(\Rightarrow36-4m+8>0\Leftrightarrow44>4m\Leftrightarrow11>m\)
Câu D
Công thức tổng quát:(n(n+3))/((n+1)(n+2))
=((n(n+3))/(n+1))-((n(n+3))/(n+2))
=n(1+2/(n+1) -1-1/(n+2))
=1-2/(n+1) +2/(n+2)
=>N=1-2/2+2/3+1-2/3+2/4+1-2/4+2/5+1-2/99+2/100
=97+2/100=4851/50