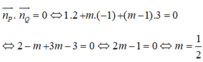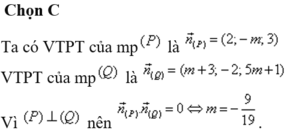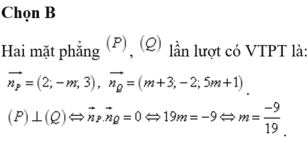Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{n_{\left(\alpha\right)}}=\left(1;2;3\right)\)
\(\overrightarrow{n_{\left(P\right)}}=\left(2;4;6\right)\)
\(\overrightarrow{n_{\left(R\right)}}=\left(2;-4;6\right)\)
\(\overrightarrow{n_{\left(Q\right)}}=\left(1;-1;2\right)\)
\(\overrightarrow{n_{\left(S\right)}}=\left(1;-1;2\right)\)
Tích vô hướng của \(\overrightarrow{n_{\left(\alpha\right)}}\) với cả 4 vecto kia đều khác 0 nên ko mặt phẳng nào vuông góc với \(\left(\alpha\right)\)
Bạn coi lại đề bài

Chọn A
Sử dụng tính chất: Nếu đường thẳng a vuông góc mặt phẳng (P) thì mọi mặt phẳng qua a đều vuông góc
(P) để nhận xét mối quan hệ giữa các mặt phẳng ![]()

Ta có:
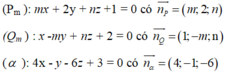
Do đó
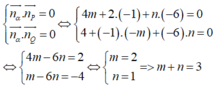

Đáp án D
Hai mặt phẳng đã cho song song khi và chỉ khi tồn tại một số thực k sao cho:
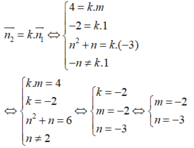

Câu 1:
Gọi A là một điểm chung của \(\left(P\right)\) và \(\left(Q\right)\) \(\Rightarrow A\in d\), chọn \(A\left(0;-1;0\right)\)
Ta có: \(\left[\overrightarrow{n_{\left(P\right)}};\overrightarrow{n_{\left(Q\right)}}\right]=\left(-2;2;0\right)=-2\left(1;-1;0\right)\)
\(\Rightarrow d\) nhận \(\overrightarrow{u_d}=\left(1;-1;0\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=t\\y=-1-t\\z=0\end{matrix}\right.\)
Câu 2:
a/ Do \(\left(Q\right)\perp d\Rightarrow\) (Q) nhận \(\overrightarrow{n_{\left(Q\right)}}=\overrightarrow{u_d}=\left(1;-2;1\right)\) là 1 vtpt
Phương trình (Q):
\(1\left(x-1\right)-2\left(y+1\right)+1\left(z-0\right)=0\Leftrightarrow x-2y+z-3=0\)
b/
Giao điểm B của \(d\) và (P):
\(1+t+1-2t-t+1=0\Rightarrow t=\frac{3}{2}\Rightarrow B\left(\frac{5}{2};-2;\frac{3}{2}\right)\)
Gọi (R) là mặt phẳng chứa d và vuông góc (P)
\(\left[\overrightarrow{u_d};\overrightarrow{n_{\left(P\right)}}\right]=\left(-1;-2;-3\right)\Rightarrow\left(R\right)\) nhận \(\overrightarrow{n_{\left(R\right)}}=\left(1;2;3\right)\) là 1 vtpt
\(\left[\overrightarrow{n_{\left(R\right)}};\overrightarrow{n_{\left(P\right)}}\right]=\left(-5;4;1\right)\) \(\Rightarrow\) hình chiếu d' của d lên (P) nhận \(\overrightarrow{u_{d'}}=\left(-5;4;1\right)\) là 1 vtcp
Phương trình \(d':\) \(\left\{{}\begin{matrix}x=\frac{5}{2}-5t\\y=-2+4t\\z=\frac{3}{2}+t\end{matrix}\right.\)

Chọn D.
Vecto pháp tuyến của hai mặt phẳng (P) và (Q) lần lượt là:
![]()
Để 2 mặt phẳng (P); (Q) vuông góc: