Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Động năng: \(W_đ=\dfrac{1}{2}mv^2\)
Khi \(v=0,5v_{max}\)
\(\Rightarrow W_đ=0,5^2.W=0,25W\)
\(\Rightarrow \dfrac{W_đ}{W}=\dfrac{1}{4}\)

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

x=Acos(\(\omega t+\varphi\))
Tại thời điểm t=0, ta có:
\(\frac{A}{2}=Acos\left(\varphi\right)\) \(\Rightarrow\)\(\varphi=-\frac{\pi}{6}\)(do vật chuyển động theo chiều dương)
\(\Rightarrow\) \(x=Acos\left(\omega t-\frac{\pi}{6}\right)\)
cái này mình tưởng phải bằng: x=Acos(\(\omega t+\frac{\pi}{3}\)) chứ.

Hướng dẫn bạn:
- Lực kéo về: \(F=k.x=0,03\sqrt 2\pi\) (không biết có đúng như giả thiết của bạn không)
\(\Rightarrow x =\dfrac{0,03\sqrt 2\pi}{k}=\dfrac{0,03\sqrt 2\pi}{m.\omega^2}=\dfrac{0,03\sqrt 2\pi}{0,01.\omega^2}=\dfrac{3\sqrt 2\pi}{\omega^2}\)
- Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 0,05^2=(\dfrac{3\sqrt 2\pi}{\omega^2})^2+\dfrac{(0,4\pi)^2}{\omega^2}\)
Bạn giải pt trên tìm \(\omega \) và suy ra chu kì \(T\) nhé.

Độ dời bằng 10% biên độ thì \(|x|=0,1.A\)
A. Do \(a=-\omega^2.x\) nên gia tốc tỉ lệ với li độ, do vậy \(|a|=0,1.A_{max}=10\%.A_{max}\) -->Sai
B. Ta có: \((\dfrac{x}{A})^2+(\dfrac{v}{v_{max}})^2=1\) \(\Rightarrow (0,1)^2+(\dfrac{v}{v_{max}})^2=1\)\(\Rightarrow (\dfrac{v}{v_{max}})^2=0,99\)
\(\Rightarrow \dfrac{v}{v_{max}}=0,995=99,5\%\) -->Đúng.
Vậy chọn B, các ý khác bạn tự thử nhé :)

\(Acos\left(\omega t=\varphi\right)\)
\(v=-A\omega sin\left(\omega t+\varphi\right)\)
\(a=-A\omega^2cos\left(\omega t+\varphi\right)\)
t = 0
\(x=Acos\varphi=-\sqrt{2}\)
\(v=-A\omega sin\varphi=-\pi\sqrt{2}\)
\(a=-A\omega^2cos\varphi=\pi^2\sqrt{2}\)
Lấy a chia cho x ta được \(\omega=\frac{\pi rad}{s}\)
v chia cho a ta được \(tan\varphi=-1\) mà cos góc này nhỏ hơn 0 nên \(\varphi=\frac{3\pi}{4}\)
A=2cm
Vậy \(x=2cos\left(\pi t+\frac{3\pi}{4}\right)cm\)

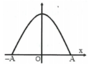
Đáp án B
*Từ đồ thị ta thấy đại lượng Y phụ thuộc vào li độ x theo một đường parabol. Do đó Y chỉ có thể là thế năng và động năng. Tuy nhiên khi li độ x=0 động năng của vật đạt cực đại và bằng cơ năng nên