Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Lăng trụ có chều cao không đổi nên có thể tích lớn nhất khi diện tích đáy lớn nhất
Đáy lăng trụ là tam giác cân có chu vi 60 cm cạnh bên là x cạnh đáy là 60 − 2 x
Diện tích đáy theo công thức Hê Rông
S = 30. 30 − x 30 − x 2 x − 30 ≤ 30. 30 − x + 30 − x + 2 x − 30 3 3 = 100 3 c m 2
Dấu bằng xảy ra ⇔ 30 − x = 2 x − 30 ⇒ x = 20 c m

Đáp án D
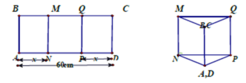
Thể tích khối trụ là V = S d . h , trong đó S d = S A N P ; h = C D không đổi.
V m a x ⇔ S d lớn nhất.
Gọi AH là chiều cao của tam giác cân ANP ( A N = A P = x ).
Khi đó
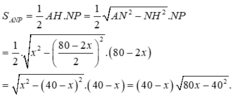
S ' = − 80 x − 40 2 + 40 − x . 40 80 x − 40 2 = − 80 x − 40 2 + 40 2 − 40 x 80 x − 40 2 = − 120 x + 2.40 2 80 x − 40 2
Bảng biến thiên:

S max = S 80 3 ≈ 307,92

Đáp án D
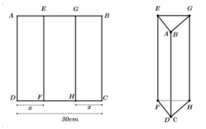
Ta có : F D = H C = x ⇒ F H = 30 − 2 x
DI ⊥ F H
Δ F D H cân tại D ⇒ S Δ F D H = 1 2 . D I . F H = 1 2 . x 2 − 30 − 2 x 2 2 . 30 − 2 x
V lăng trụ = S Δ F D H . E F = 1 2 . x 2 − 30 − 2 x 2 2 . 30 − 2 x .30
Xét hàm y = 15 30 x − 225 . 30 − 2 x điều kiện : 30 x − 225 ≥ 0 ⇔ x ≥ 15 2
y ' = 15. ( − 90 x + 900 ) 30 x − 225
Cho y ' = 0 ⇔ x = 10
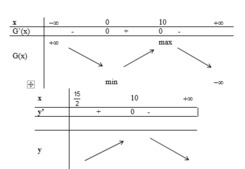
vậy V max = 10

Đáp án B
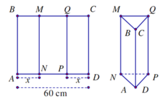
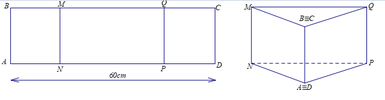
Đặt AN = PD = x suy ra NP = AD-(AN + PD) = 60 - 2x
Gọi H là trung điểm của NP, tam giác ANP cân ⇒ A H ⊥ N P . Suy ra diện tích tam giác ANP là S ∆ A N P = 1 2 . A H . N P = 1 2 . A N 2 - N H 2 . N P = 1 2 A N 2 - N P 2 4 . N P = 1 2 . x 2 - 60 - 2 x 2 4 . 60 - 2 x = 1 2 . 60 x - 900 . 60 - 2 x . . Thể tích khối lăng trụ ANP.BMQ là V = A B . S ∆ A N P = A B . 15 x - 225 . 60 - 2 x . Xét hàm số f x = 30 - x x - 15 trên đoạn [15;30] suy ra m i n [ 15 ; 30 ] f x = 10 5 . Dấu bằng xảy ra khi và chỉ khi x = 20. Vậy độ dài AN = 20 cm.

Đáp án B
Gọi R, h lần lượt là bán kính đáy và chiều cao của khối trụ
Chọ hệ trục tọa độ Oxy như hình vẽ với tứ giác ABCD là hình chữ nhật nối tiếp hình (E)

Gọi A x 0 ; y 0 x 0 > y 0 > 0 , khi đó ta có A B = 2 π R C D = h ⇔ 2 x 0 = 2 π R 2 y 0 = h ⇔ x 0 = π R y 0 = h 2
Thể tích khối trụ là V = π R 2 h = 2 x 0 2 π . y 0 mà A ∈ E ⇒ x 0 2 a 2 + y 0 2 b 2 = 1 ⇒ x 0 2 = a 2 b 2 b 2 − y 0 2

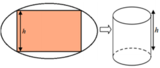
Gọi chiều dài tấm tôn là x (cm) (0 < x < 60) Suy ra chiều rộng: 60 - x (cm)
Giả sử quấn tấm tôn theo cạnh có kích thước x => bán kính đáy r = x 2 π và chiều cao h = 60 - x
Khi đó
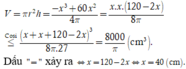
Chọn C.

Đáp án A
Phương pháp:
Tính độ dài các đoạn thẳng MN và MQ sau đó áp dụng công thức tình thể tích hình trụ V = π r 2 h


Đáp án B.
Qua O kẻ đường thẳng vuông góc với MN, đường thẳng này cắt MN, PQ, cung AB,AQ lần lượt tại H,F,D,E
Độ dài cung AB là chu vi đường tròn đáy của hình nón nên
l A B = 2 πr = 2 π . 2 3 = 4 π 3
Lại có l a b = α . O A ⇒ α = l a b O A = 4 π 3 : 2 = 2 π 3 = A O B ⏜
Áp dụng định lý cosin trong tam giác OAB có
A B = O A 2 + O B 2 - 2 . O A . O B . cos A O B ⏜ = 2 2 + 2 2 - 2 . 2 2 - 1 2 = 2 3
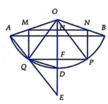 Do M,N lần lượt là trung điểm của OA,OB nên
A
O
B
⏜
⇒
A
O
D
⏜
=
60
°
Do M,N lần lượt là trung điểm của OA,OB nên
A
O
B
⏜
⇒
A
O
D
⏜
=
60
°
⇒ M H = 1 2 M N = 3 2
Do O D ⊥ A B nên OD là tia phân giác của A O B ⏜ ⇒ A O D ⏜ = 60 ° . Xét tam giác vuông OMH có O H = O M . cos 60 = 1 . 1 2 = 1 2
Xét tam giác OPQ có cos P O Q ⏜ = O P 2 + O Q 2 - P Q 2 2 . O P . O Q = 2 2 + 2 2 - 3 2 2 . 2 . 2 = 5 8
Mà cos P O Q ⏜ = cos 2 D O Q ⏜ = 2 cos 2 D O Q ⏜ - 1 = 5 8 ⇒ cos D O Q ⏜ = 13 4
Xét tam giác DOQ có:
Q D 2 + O Q 2 + O D 2 - 2 . O Q . O D . cos D O Q ⏜ = 8 - 2 13
Xét tam giác vuông DQF có
D F 2 = Q D 2 - Q F 2 = 8 - 2 13 - 3 2 2 = 29 4 - 2 13
⇒ D F = 29 - 8 13 2 = 4 - 13 2 2 = 4 - 13 2
⇒ H F = O D - O H - D F = 2 - 1 2 - 4 - 13 2 = 13 - 1 2 = M Q - N P
Gọi R là bán kính đáy của hình trụ tạo bởi hình chữ nhật MNPQ. Chu vi đáy của hình trụ chính là độ dài của PQ nên P Q = 2 πR → R = 3 2 π
Khi đó thể tích khối trụ tạo ra bởi hình chữ nhật MNPQ là:
V = πR 2 . MQ = π 3 2 π 2 . 13 - 1 2 = 3 13 - 1 8 π

Đáp án là D.
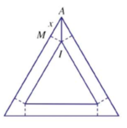
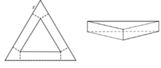
M I = x 3 3 ; S t g = a − 2 x 2 3 4 .
V l t = M I . S t g = a 2 x − 4 a x 2 + 4 x 3 4 ; 0 < x < a 2 .
xét hàm số
f x = 4 x 3 − 4 a x 2 + a 2 x ⇒ f ' x = 12 x 2 − 8 a x + a 2 , cho f ' x = 0 ⇔ x = a 6 x = a 2 l o a i
Thể tích đạt GTLN khi x = a 6 .

Đáp án A
Thể tích lớn nhất khi diện tích tam giác NPD là lớn nhất, điều này xảy ra khi tam giác đó là tam giác đều (vì chu vi là không đổi) tức là x=20cm